Solution of Fractional Order Equations in the Domain of the Mellin Transform

Authors

Keywords:

Caputo fractional derivative, Fractional calculus, Mellin transform, Miller-Ross fractional derivative, Riemann-Liouville fractional derivative, Riemann-Liouville fractional integral

Abstract

This paper presents the Mellin transform for the solution of the fractional order equations. The Mellin transform approach occurs in many areas of applied mathematics and technology. The Mellin transform of fractional calculus of different flavours; namely the Riemann-Liouville fractional derivative, Riemann-Liouville fractional integral, Caputo fractional derivative and the Miller-Ross sequential fractional derivative were obtained. Three illustrative examples were considered to discuss the applications of the Mellin transform and its fundamental properties. The results show that the Mellin transform is a good analytical method for the solution of fractional order equations.

Dimensions

A. A. Kilbas, H. M. Srivastava & J. J. Trujillo, Theory and applications of fractional differential equations, (2006) Elsevier, Amsterdam, Netherland.

A. A. Elbeleze, A. Kilicman and B. M. Taib, "Homotopy pertubation method for fractional Black-Scholes European option pricing equations using Sumudu transform, Mathematical Problems in Engineering, 2013 (2013) 1.

I. Podlubny, Fractional differential equations. An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, 198 (1999), Mathematics in Science and Engineering, Academic press.

S. E. Fadugba, "Closed-Form Solution of Generalized Fractional Black-Scholes-Like Equation using Fractional Reduced Differential Transform Method and Fractional Laplace Homotopy Perturbation Method", International Journal of Engineering and Future Technology 16 (2019) 13.

S. Kumar, A. Yildirim, Y. Khan, H. Jafari, K. Sayevand & L. Wei, "Analytical solution of fractional Black-Scholes European option pricing equation by using Laplace transform", Journal of Fractional Calculus and Applications 2 (2012) 1.

Ch. Friedrich, "Relaxation and retardation functions of the Maxwell model with fractional derivatives", Rheologica Acta 30 (1991) 151.

R. L. Bagley & R. A. Calico, "Fractional-order state equations for the control of viscoelastically damped structures", J. Guidance 14 (1991) 304.

K. S. Miller & B. Ross, "An Introduction to the Fractional Calculus and Fractional Differential Equations, (1993), John Wiley and Sons Inc., New York.

K. B. Oldham, C. G. Zoski, ``Analogue instrumentation for processing polarographic data", Electroanal. Chem. 157 (1983) 27.

A. Kilicman, "A note on Mellin transform and distributions", Math. Comput. Appl. 9 (2004) 65.

A. Erdelyi, W. Magnus, F. Oberhettinger & F. Tricomi, Tables of integral transforms, (1954), First edition, McGraw-Hill, New York.

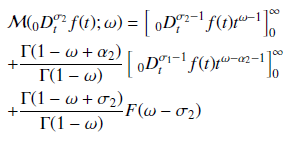
Published

2019-12-30

How to Cite

Solution of Fractional Order Equations in the Domain of the Mellin Transform. (2019). Journal of the Nigerian Society of Physical Sciences, 1(4), 138-142. https://doi.org/10.46481/jnsps.2019.31

Issue

Volume 1, Issue 4, November 2019

Section

Original Research
Copyright & Licensing

Copyright (c) 2019 Journal of the Nigerian Society of Physical Sciences

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Solution of Fractional Order Equations in the Domain of the Mellin Transform. (2019). Journal of the Nigerian Society of Physical Sciences, 1(4), 138-142. https://doi.org/10.46481/jnsps.2019.31