On Some Pursuit Differential Game Problem in a Hilbert Space

Authors

  • Jamilu Adamu Department of Mathematics, Federal University, Gashua, Nigeria
  • Aminu Sulaiman Halliru Department of Mathematical Sciences, Bayero University, Kano, Nigeria
  • Bala Ma’aji Abdulhamid Department of Mathematical Sciences, Abubakar Tafawa Balewa University, Bauchi, Nigeria.

Keywords:

Differential Game. pursuers. Evader.Integral constraint.Geometric constraint. Hilbert space.

Abstract

Abstract We study pursuit differential game problem in which a countable number of pursuers chase one evader. The problem is formulated in a Hilbert space l2 with pursuers’ motions described by nth order differential equations and that of the evader by mth order differential equation. The control functions of the pursuers and evader are subject to integral and geometric constraints respectively.Duration of the game is denoted by the positive number?. Pursuit is said to be completed if there exist strategies uj of the pursuers Pj such that for any admissible control v(·) of the evader E the inequality ky(?) ? xj (?)k ? rj is satisfied for some j ? {1, 2, . . .}. In this paper, sufficient condition for completion of pursuit were obtained and also strategies of the pursuers that ensure completion of pursuit are constructed.

Dimensions

J. Adamu, K. Muangehoo, A. J. Badakaya and J. Rilwan, ”On pursuitevasion differential game problem in a Hilbert space”, AIMS mathematics 5 (2020) 7467.

A. J Badakaya, ”A Pursuit Differential Game Problems with Different Constraints on the Control of the Players”, Transaction of the Nigerian Association of Mathematical Physics 8 (2019) 17.

G. I. Ibragimov and B. B. Rikhsiev, ”On some Sufficient Conditions for Optimalty of the Pursuit Time in the Differential Game with Multiple Pusuers”, Automation and Remote Control 67 (2006) 529.

J. Adamu, B. M. Abdulhamid, D. T. Gbande and A. S. Halliru, ”Simple motion pursuit di erential game”, Journal of the Nigerian Society Physical Sciences 3 (2021) 12.

G. I. Ibragimov and N. A. Hussin, ”A Pursuit-Evasion Differential Game with Many Pursuers and One Evader”, Malaysian Journal of Mathematical Sciences 4 (2010) 183.

G. I. Ibragimov and M. Salimi, ”Pursuit-Evasion Differential Game with Many Inertial Players”, Mathematical Problems in Engineering 2009 (2009) 15.

G. I. Ibragimov, A. Sh. Kuchkarov, ”Fixed Duration Pursuit-Evasion Differential Game with Integral Constraints”, Journal of Physics Conference Series 435 (2017).

G. I. Ibragimov, ”Optimal pursuit with Countably Many Pursuers and one Evader”, Differential Equations 41 (2005) 627.

G. I. Ibragimov, ”Simple motion pursuit differential game of many pursuersand one evader on convex compact set”, International Journal of pure and Applied Mathematics 4 (2015) 733.

G. I. Ibragimov and N. Satimov, ”A Multiplayer Pursuit Differential Game on a Convext Set with Integral Constraints”, Abstract and Applied Analysis, 2012 (2012) doi: 10.1155/2012/460171.

G. I. Ibragimov, and A. I. Alias, ”A pursuit problem described by infinite system of di erential equations with coordinate-wise integral constraints on control functions”, Malaysian Journal of Applied Mathematical Sciences

(2015) 67.

W. J. Leong, and G. I. Ibragimov, ”A multiperson pursuit problem on a closed convex set in Hilbert spaces”, Far East Journal of Applied Mathematics 33 (2008) 205.

A. Kuchkarov, G. I. Ibragimov and M. Ferrara, ”Simple Motion Pursuit and Evasion Di erential Games with Many Pursuers on Manifolds with Euclidean Metric”, Discrete Dynamics in Nature and Society 2016 (2016)

http://dx.doi.org/10.1155/2016/1386242.

A. B. Jaafaru and G. I. Gafurjan, ”On Some Pursuit and Evasion Differential Game Problems for an Infinite Number of First-Order Differential Equations”, Journal of Applied Mathematics 2012 (2012) 13.

A. B. Jaafaru and G. I. Gafurjan, ”Differential Game described by Infinite system of DE’S of 2nd Order. The case of negetive coefficients”, International Journal of Pure and Applied Mathematics 70 (2011) 927.

M. Salimi, G. I. Ibragimov, S. Stefen and S. Somayeh, ”On a fixed duration Pursuit di erential game with geometric and integral constraints”, Dyn Games Appl. 2015 (2015) doi.org/10.1007/s 13235-015-0161-3.

G. I. Ibragimov, N. Abd Rashid, A. Kuchkarov and F. Ismail,” Multi Pursuer Differential Game of Optimal Approach with Integral Constraints on Controls of the Players”, Taiwanese Journal of Mathematics 19 (2015)

G. I. Ibragimov, ”A Game of Optimal Pursuit of One Object by Several”, Journal of Applied Mathematics and Mechanics 62 (1988) 187.

G. I. Ibragimov, ”Game Problem on a closed convex set”, Siberian Advances in Mathematics 12 (2002) 16.

R. P. Ivanov and Yu. S. Ledyaev, ”Optimality of pursuit time in a simple motion di erential game of many objects”, Trudy Matematicheskogo Instituta imeni V. A. Steklova 158 (1981) 87.

N. Siddiqoba, S. Muksimova, A. Rakhmanov,” Research of One Problem of Different Constraints on the Controls”, International Journal of Scientific and Research Publications 7 (2017) 65.

B. T. Samatov,” Problems of Group Pursuit with Integral Constraints on Controls of the Players” I, Cybernetics and System Analysis 49 (2013) 756.

M. Salimi and M. Ferrara, ”Differential Game of Optimal Pursuit of one Evader by Many Pursuers”, International Journal of Game Theory 48 (2019) 481.

A. YU. Levchenkov and A. G. Pashkov, ”Differential Game of Optimal Approach of Two Inertial Pursuers to a Noninertial Evader”, Journal of Optimization Theory and Applications 65 (1990) 501.

D. A. Vagin and N. N. Petrov, ”A Problem of Group Pursuit with Phase Constraints”, Journal of Applied Mathematics and Mechanics 66 (2002) 225.

A. I. Subbotin, and A. G. Chentsov, Optimazition of Guaranteed Result in Control Problem, Moscow, Russia, 1981.

W. Abdul-majid, Linear and Nonlinear Integral Equation Methods and Applications, 10-20, Saints Xavier University, Chicago , 11,60655, USA, 2011.

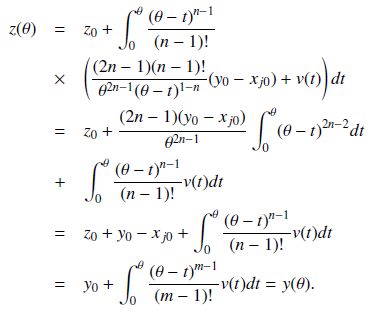
Published

2022-02-27

How to Cite

On Some Pursuit Differential Game Problem in a Hilbert Space. (2022). Journal of the Nigerian Society of Physical Sciences, 4(1), 83-87. https://doi.org/10.46481/jnsps.2022.379

Issue

Volume 4, Issue 1, February 2022

Section

Original Research
Copyright & Licensing

Copyright (c) 2022 Journal of the Nigerian Society of Physical Sciences

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

On Some Pursuit Differential Game Problem in a Hilbert Space. (2022). Journal of the Nigerian Society of Physical Sciences, 4(1), 83-87. https://doi.org/10.46481/jnsps.2022.379