Statistical Modelling by Topological Maps of Kohonen for Classification of the Physicochemical Quality of Surface Waters of the Inaouen Watershed Under Matlab

Authors

  • R. El chaal Engineering Sciences Laboratory. Data Analysis, Mathematical Modeling, and Optimization Team, Department of Computer Science, Logistics and Mathematics, Ibn Tofail University National School of Applied Sciences ENSA, Kenitra 14 000 Morocco
  • M. O. Aboutafail Engineering Sciences Laboratory. Data Analysis, Mathematical Modeling, and Optimization Team, Department of Computer Science, Logistics and Mathematics, Ibn Tofail University National School of Applied Sciences ENSA, Kenitra 14 000 Morocco

Keywords:

Classification, Self-Organizing maps, SOM, Physical-Chemical parameters, Cluster

Abstract

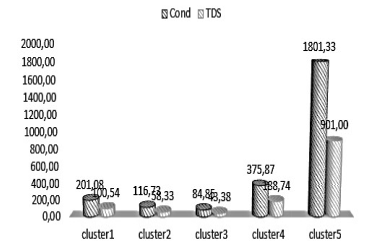
Self-organizing maps (SOMs) and other artificial intelligence approaches developed by Kohonen can be used to model and solve environmental challenges. To emphasize the classification of Physico-chemical parameters of the Inaouen watershed, we presented a classification strategy based on a self-organizing topological map (SOM) artificial neural network in this study. The use of a self-organizing map to classify samples resulted in the following five categories: Low quantities of Sodium Na (mg/l), Potassium k(mg/l), Magnesium Mg(mg/l), Calcium Ca(mg/l), Sulfates SO4(mg/l), and Total Dissolved Solids TDS (mg/l) distinguish Classes 2 and 3. Bicarbonate HCO3 (mg/l), Total Dissolved Solids TDS (mg/l), Total Alkalinity CaCO3(mg/l), Mg(mg/l), Calcium Ca (mg/l), and electrical conductivity Cond (ms/cm) are slightly greater in Classes 1 and 4. Except for Dissolved Oxygen D.O. (mg/l) and Nitrate NO3(mg/l), Class 5 has exceptionally high values for all metrics. The results suggest that Kohonen's self-organizing topological maps (SOM) classification is an outstanding and fundamental tool for understanding and displaying the spatial distribution of water physicochemical quality.

 

Dimensions

T. Kohonen, Self-Organizing Maps, 3rd ed., 30, Berlin, Heidelberg: Springer Berlin Heidelberg, (2001).

S. Qu, Z. Shi, X. Liang, G. Wang, and J. Han, “Multiple factors control groundwater chemistry and quality of multi-layer groundwater system in Northwest China coalfield - Using self-organizing maps (SOM),” J. Geochemical Explor. 227 (2021) 106795. doi:10.1016/j.gexplo.2021.106795.

A. Bigdeli, A. Maghsoudi, and R. Ghezelbash, “Application of self-organizing map (SOM) and K-means clustering algorithms for portraying geochemical anomaly patterns in Moalleman district, NE Iran,” J. Geochemical Explor. 233 (2022) 106923. doi:10.1016/j.gexplo.2021.106923.

M. R. Santos, A. Roisenberg, F. Iwashita, and M. Roisenberg, “Hydrogeochemical spatialization and controls of the Serra Geral Aquifer System in southern Brazil: A regional approach by self-organizing maps and k-means clustering,” J. Hydrol. 591 (2020) 125602. doi:10.1016/j.jhydrol.2020.125602.

V. Amiri and K. Nakagawa, “Using a linear discriminant analysis (LDA)-based nomenclature system and self-organizing maps (SOM) for spatiotemporal assessment of groundwater quality in a coastal aquifer,” J. Hydrol. 603 (2021) 127082. doi:10.1016/j.jhydrol.2021.127082.

B. Benzougagh, A. Dridri, L. Boudad, D. Sdkaoui, and B. Baamar, “Contribution of GIS and remote Sensing for the evaluation of the physical characteristics of Inaouene watershed (northeast Morocco) and their uses in the field of natural hazard management,” Am. J. Innov. Res. Appl. Sci. (2019) 120. [Online]. Available: www.american-jiras.com.

R. El Chaal and M. O. Aboutafail, “Development of Stochastic Mathematical Models for the Prediction of Heavy Metal Content in Surface Waters Using Artificial Neural Network and Multiple Linear Regression,” E3S Web Conf. 314 (2021) 02001. doi:10.1051/e3sconf/202131402001.

O. Olubi, E. Oniya, and T. Owolabi, “Development of Predictive Model for Radon-222 Estimation in the Atmosphere using Stepwise Regression and Grid Search Based-Random Forest Regression,” J. Niger. Soc. Phys. Sci. 3 (2021) 132. doi: 10.46481/jnsps.2021.177.

T. Kohonen, “The self-organizing map,” Neurocomputing 21 (1998) 1. doi: 10.1016/S0925-2312(98)00030-7.

David Opeoluwa Oyewola, E. G. Dada, J. N. Ndunagu, T. Abubakar Umar, and A. S.A, “COVID-19 Risk Factors, Economic Factors, and Epidemiological Factors nexus on Economic Impact: Machine Learning and Structural Equation Modelling Approaches,” J. Niger. Soc. Phys. Sci. 3 (2021) 395. doi: 10.46481/jnsps.2021.173.

V. Umarani, A. Julian, and J. Deepa, “Sentiment Analysis using various Machine Learning and Deep Learning Techniques,” J. Niger. Soc. Phys. Sci. 3 (2021) 385. doi: 10.46481/jn-sps.2021.308.

N. P. Rougier and G. I. Detorakis, “Randomized Self-Organizing Map,” Neural Comput. 33 (2021) 2241. doi: 10.1162/neco_a_01406.

D. Olszewski, “A data-scattering-preserving adaptive self-organizing map,” Eng. Appl. Artif. Intell. 105 (2021) 104420. doi:10.1016/j.engappai.2021.104420.

N. Vassilas, “Self-organization of the batch Kohonen network under quantization effects,” Int. J. Comput. Math. 88 (2011) 3586. doi: 10.1080/00207160.2011.620094.

J. Oyelade et al., “Data Clustering: Algorithms and Its Applications,” in 2019 19th International Conference on Computational Science and Its Applications (ICCSA), Jul. (2019) 71., doi: 10.1109/ICCSA.2019.000-1.

R. Ponmalai and C. Kamath, Self-Organizing Maps and Their Applications to Data Analysis. U.S, 2019.

G. Cabanes and Y. Bennani, “Learning Topological Constraints in Self-Organizing Map,” NEURAL INFORMATION PROCESSING: MODELS AND APPLICATIONS, PT II 6444 17th International Conference on Neural Information Processing (2010) 367.

H. Ritter, “Self-Organizing Maps on non-euclidean Spaces,” in Kohonen Maps, Elsevier (1999) 97.

E. A. Uriarte and F. D. Martin, “Topology Preservation in SOM,” PROCEEDINGS OF WORLD ACADEMY OF SCIENCE, ENGINEERING AND TECHNOLOGY, VOL 15, no. Conference of the World-Academy-of-Science-Engineering-and-Technology. Univ Deusto, Fac Engn, Bilbao, Spain NR - 20 PU - WORLD ACAD SCI, ENG & TECHWASET PI - CANAKKALE PA - PO BOX 125, CANAKKALE, 17100, TURKEY, pp. 187-190 WE-Conference Proceedings (2006).

K. Kiviluoto and IEEE, “Topology preservation in self-organizing maps,” ICNN - 1996 IEEE INTERNATIONAL CONFERENCE ON NEURAL NETWORKS, IEEE International Conference on Neural Networks (ICNN 96) 1-4 (1996) 294.

A. B. Yusuf, R. M. Dima, and S. K. Aina, “Optimized Breast Cancer Classification using Feature Selection and Outliers Detection,” J. Niger. Soc. Phys. Sci. 3 (2021) 298. doi:10.46481/jnsps.2021.331.

D. Umar, O. V. Omonona, and C. Okogbue, “Groundwater Quality Assessment Using Multivariate Analysis and Water Quality Index in some Saline Fields of Central Nigeria,” J. Niger. Soc. Phys. Sci. 3 (2021) 267. doi: 10.46481/jnsps.2021.183.

F. K. Nakano, R. Cerri, and C. Vens, “Active learning for hierarchical multi-label classification,” Data Min. Knowl. Discov. 34 (2020) 1496. doi: 10.1007/s10618-020-00704-w.

J. L. Giraudel and S. Lek, “A comparison of self-organizing map algorithm and some conventional statistical methods for ecological community ordination,” Ecol. Modell. 146 (2001) 329. doi: 10.1016/S0304-3800(01)00324-6.

J. Serrano-Pérez and L. E. Sucar, “Artificial datasets for hierarchical classification,” Expert Syst. Appl. 182 (2021) 115218. doi:10.1016/j.eswa.2021.115218.

C. Luo, T. Li, H. Chen, H. Fujita, and Z. Yi, “Incremental rough set approach for hierarchical multicriteria classification,” Inf. Sci. (Ny). 429 (2018) 72. doi:10.1016/j.ins.2017.11.004.

H. Zhao, S. Guo, and Y. Lin, “Hierarchical classification of data with long-tailed distributions via global and local granulation,” Inf. Sci. (Ny). 581 (2021) 536. doi:10.1016/j.ins.2021.09.059.

Z.-P. Lo and B. Bavarian, “On the rate of convergence in topology preserving neural networks,” Biol. Cybern. 65 (1991) 55. doi:10.1007/BF00197290.

M. Roux, “A Comparative Study of Divisive and Agglomerative Hierarchical Clustering Algorithms,” J. Classif. 35 (2018) 345. doi:10.1007/s00357-018-9259-9.

N. Randriamihamison, N. Vialaneix, and P. Neuvial, “Applicability and Interpretability of Ward’s Hierarchical Agglomerative Clustering With or Without Contiguity Constraints,” J. Classif. 38 (2021) 363. doi: 10.1007/s00357-020-09377-y.

Published

2022-05-29

How to Cite

Statistical Modelling by Topological Maps of Kohonen for Classification of the Physicochemical Quality of Surface Waters of the Inaouen Watershed Under Matlab. (2022). Journal of the Nigerian Society of Physical Sciences, 4(2), 223-230. https://doi.org/10.46481/jnsps.2022.608

Issue

Volume 4, Issue 2, May 2022

Section

Original Research
Copyright & Licensing

Copyright (c) 2022 Journal of the Nigerian Society of Physical Sciences

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Statistical Modelling by Topological Maps of Kohonen for Classification of the Physicochemical Quality of Surface Waters of the Inaouen Watershed Under Matlab. (2022). Journal of the Nigerian Society of Physical Sciences, 4(2), 223-230. https://doi.org/10.46481/jnsps.2022.608