Implicit Four-Point Hybrid Block Integrator for the Simulations of Stiff Models

Authors

  • J. Sunday Department of Mathematics, University of Jos, Jos 930003, Nigeria
  • G. M. Kumleng Department of Mathematics, University of Jos, Jos 930003, Nigeria
  • N. M. Kamoh Department of Mathematics, University of Jos, Jos 930003, Nigeria
  • J. A. Kwanamu Department of Mathematics, Adamawa State University, Mubi 650001, Nigeria,
  • Y. Skwame Department of Mathematics, Adamawa State University, Mubi 650001, Nigeria
  • O. Sarjiyus Department of Computer Science, Adamawa State University, Mubi 650001, Nigeria

Keywords:

Hybrid block integrator, Imolicit, Lagrange polynomial, Simulation, Stiff model

Abstract

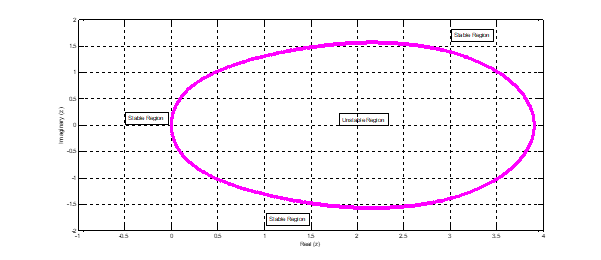
Over the years, the systematic search for stiff model solvers that are near-optimal has attracted the attention of many researchers. An attempt has been made in this research to formulate an implicit Four-Point Hybrid Block Integrator (FPHBI) for the simulations of some renowned rigid stiff models. The integrator is formulated by using the Lagrange polynomial as basis function. The properties of the integrator which include order, consistency, and convergence were analyzed. Further analysis showed that the proposed integrator has an A-stability region. The A-stability nature of the integrator makes it more robust and fitted for the simulation of stiff models. To test the computational reliability of the new integrator, few well-known technical stiff models such as the pharmacokinetics, Robertson and Van der Pol models were solved. The results generated were then compared with those of some existing methods including the MATLAB solid solvent, ode 15s. From the results generated, the new implicit FPHBI performed better than the ones with which we compared our results with.

Dimensions

Dahlquist, G.G. A special stability problem for linear multistep methods. BIT Numerical Mathematics 1963, 3, 27-43.

Ijam H.M., Ibrahim Z.B., Majid Z.A., Senu Z. Stability analysis of a diagonally implicit scheme of block backward differentiation formula for stiff pharmacokinetics models. Advances in Difference Equations 2020, 400.

Henrici P. Discrete variable methods in ordinary differential equations. John Wiley and Sons Inc.: Hoboken, NJ, USA, 1969.

Aiken, R. Stiff computations. Oxford University Press: New York, NY, USA, 1985.

Sandu A., Verwer J.G., Blom J.G., Spee E.J., Carmichael G.R., Potra F.A. Benchmarking stiff ordinary differential equation solvers for atmospheric chemistry problem II: Rosenbrock Solvers. Atmos. Environ. 1997, 31, 3459-3479.

Kin J., Cho S.Y. Computational accuracy and efficiency of the time-splitting method in solving atmospheric transport/chemistry equations. Atmos. Environ. 1997, 31, 2215-2224.

Amat S., Legaz M.J., Ruiz-Alvarez, J. On a Variational method for stiff differential equations arising from chemistry kinetics. Mathematics 2019, 7, 459.

Ibrahim, Z.B., Nasarudin, A.A. A class of hybrid multistep block methods with A-stability for the numerical solution of stiff ordinary differential equations. Mathematics 2020, 8,914, 1-19.

Nasarudin , A.A., Ibrahim, Z.B., Rosali, H. On the integration of stiff ordinary differential equations using block backward differential formulas of order six. Symmetry 2020, 12, 1-13.

Curtis C.F., Hirschfelder J.O. Integration of stiff equations. Proc. Natl. Acad. Sc. USA 1952, 38, 235-243.

Hoffman J.D. Numerical methods for engineers and scientists; Marcel Dekker Inc.: New York, USA, 2001.

Lambert, J.D. Numerical methods for ordinary differential systems: The initial value problem. John Wiley and Sons LTD, United Kingdom, 1991.

Hairer H, Wanner G. Solving ordinary differential equations II. Springer, Berlin/Heidelberg, Germany, pp. 2, 1996.

Lambert J.D. Computational methods in ordinary differential equations. John Wiley and Sons: Hoboken, NJ, USA, 1973; pp.22-23, 231-233.

Enright W.H. Second derivative multistep methods for stiff ordinary differential equations. SIAM Journal of Numerical Analysis 1974, 11, 321-331.

Khalsaraei M.M., Shokri A., Molayi M. The new high approximation of stiff systems of first order IVPs arising from chemical reactions by k-step L-stable hybrid methods. Iranian Journal of Mathematical Chemistry 2019, 10(2), 181-193.

Soomro, H., Zainuddin, N., Daud, H., Sunday, J. Optimized hybrid block Adams method for solving first order ordinary differential equations. Computers, Materials & Continua 2022, 72(2), 2947-2961.

Ajileye, G., Amoo, S.A., Ogwumu, O.D. Two-step hybrid block method for solving first order ordinary differential equations using power series approach. Journal of advances in Mathematics and Computer Science 2018, 28(1), 1-7.

Ibrahim Z.B., Ijam H.M. Diagonally implicit block backward differentiation formula with optimal stability properties for stiff ordinary differential equations. Symmetry 2019, 11, 1342.

Ibrahim, Z.B., Noor, N.M., Othman, K.I. Fixed coefficient stable block backward differentiation formulas for stiff ordinary differential equations. Symmetry 2019, 11, 1-12

Kashkari, B.S.H, Syam, M.I. Optimization of one-step block method with three hybrid points for solving first-order ordinary differential equations. Results in Physics 2019, 12, 592-596.

Ogunniran, M.O., Haruna, Y., Adeniyi, R.B., Olayiwola, M.O. Optimized three-step hybrid block method for stiff problems in ordinary differential equations. Journal of Science and Engineering 2020, 17(2), 80-95.

Khalsaraei, M.M.; Shokri, A.; Molayi, M. The new class of multistep multiderivative hybrid methods for the numerical solution of chemical stiff systems of first order IVPs. Journal of Mathematical Chemistry 2020, 58, 1987-2012.

Akinfenwa, O.A., Abdulganiy, R.I., Akinnukawe, B.I., Okunuga, S.A. Seventh order hybrid block method for solution of first order stiff order systems of initial value problems. Journal of the Egyptian Mathematical Society 2020, 28(1), 1-11.

Esuabana, I., Ekoro, S., Ojo, B., Abasiekwere, U. Adam’s block with first and second derivative future points for initial value problems in ordinary differential equations. Journal of Mathematical and Computational Sciences 2021, 11(2), 1470-1485.

Sunday, J, Chigozie, C., Omole, E.O., Gwong, J.B. A pair of three-step hybrid block methods for the solutions of linear and nonlinear first order systems. European Journal of Mathematics and Statistics 2022, 3(1), 13-23.

Soomro, H., Zainuddin, N., Daud, H., Sunday, J., Jamaludin N. Variable step block hybrid method for stiff chemical kinetics problems. Applied Sciences 2022, Accepted for publication.

Fatunla, S.O. Numerical integrators for stiff and highly oscillatory differential equations. Mathematics of Computation 1980, 34, 373-390.

Khanday M.A.m Rafiq A., Nazir K. Mathematical models for drug diffusion through the compartments of blood and tissue medium. Alexandria Journal of Medicine 2017, 53, 245-249.

Spitznagel E. Two-compartmental pharmacokinetics models. C-ODE-E. Harvey Mudd College, Fall, 1992.

Shonkwiler R.W., Herod J. Mathematical biology. An introduction with maple and matlab. Springer, Berlin, 2009.

Kanneganti K.K., Simon L. Two-compartment pharmacokinetics models for chemical engineers. ChE Curriculum 2011, 45(2), 101-105.

Shityakov S., Forster C. Pharmacokinetic delivery and metabolizing rate of nicardipine incorporated in hydrophilic and hydrophobic cyclodextrins using two-compartment mathematical model. The Science World Journal 2013, 131358, 1-13.

Robertson H. The solution of a set of reaction rate equations numerical analysis. Thompson Book Co., Washington, 1967.

Mazzia F., Cash J.R., Soetaert K. A test set for stiff initial value problem solvers in the open source software R: Package deTestset. Journal of Computational and Applied Mathematics 2012, 236(16), 4119-4131.

Tsatsos M. Theoretical and numerical study of the Van der Pol equations. PhD Dissertation, Aristotle University of Thessaloniki, Greece, 2006.

Guckenheimer J.H., Hoffman K., Weckesser W. Numerical computation of canards. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 2000, 10, 2669-2687.

Rowat P.F., Selverston A.I. Modeling the gastric mill central pattern generator of the lobster with a relaxation-oscillator network. Journal of Neurophysiology 1993, 70, 1030-1053.

Cartwright J., Eguiluz V., Hernandez-Gargia E., Piro O. Dynamics of elastic excitable media. Internat. J. Bifur. Chaos Appl. Sc. Engrg. 1999, 9, 2197-2202.

Fitzhugh R. Impulses and physiological state in theoretical models of nerve membrane. Biophysics Journal 1961, 1, 445-466.

Published

2022-05-29

How to Cite

Implicit Four-Point Hybrid Block Integrator for the Simulations of Stiff Models. (2022). Journal of the Nigerian Society of Physical Sciences, 4(2), 287-296. https://doi.org/10.46481/jnsps.2022.777

Issue

Volume 4, Issue 2, May 2022

Section

Original Research
Copyright & Licensing

Copyright (c) 2022 Journal of the Nigerian Society of Physical Sciences

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Implicit Four-Point Hybrid Block Integrator for the Simulations of Stiff Models. (2022). Journal of the Nigerian Society of Physical Sciences, 4(2), 287-296. https://doi.org/10.46481/jnsps.2022.777