The Derivation of the Riemann Analytic Continuation Formula from the Euler’s Quadratic Equation
Keywords:
Riemann zeta function, Euler’s equation, Meromorphic function, Non-trivial zerosAbstract
The analysis of the derivation of the Riemann Analytic Continuation Formula from Euler’s Quadratic Equation is presented in this paper. The connections between the roots of Euler’s quadratic equation and the Analytic Continuation Formula of the Riemann Zeta equation are also considered. The method of partial summation is applied twice on the resulting series, thus leading to the Riemann Analytic Continuation Formula. A polynomial approach is anticipated to prove the Riemann hypothesis; thus, a general equation for the zeros of the Analytic Continuation Formula of the Riemann Zeta equation based on a polynomial function is also obtained. An expression in Terms of Prime numbers and their products is considered and obtained. A quadratic function, G(tn), that is required for Euler’s quadratic equation (EQE) to give the Analytic Continuation Formula of the Riemann Zeta equation (ACF) is presented. This function thus allows a new way of defining the Analytic Continuation Formula of the Riemann Zeta equation (ACF) via this equivalent equation. By and large, the Riemann Zeta function is shown to be a type of L function whose solutions are connected to some algebraic functions. These algebraic functions are shown and presented to be connected to some polynomials. These Polynomials are also shown to be some of the algebraic functions’ solutions. Conclusively, &(z) is redefined as the product of a new function which is called H(tn; z) and this new function is shown to be dependent on the polynomial function, G(tn).
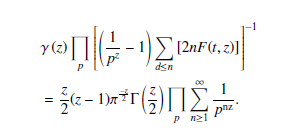
Published
How to Cite
Issue
Section
Copyright (c) 2022 Opeyemi O. Enoch, Adejimi A. Adeniji, Lukman O. Salaudeen

This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
Most read articles by the same author(s)
- Opeyemi O. Enoch, Catherine O. Alakofa , Lukman O. Salaudeen , Odd Order Integrator with Two Complex Functions Control Parameters for Solving Systems of Initial Value Problems , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 1, February 2023







