Odd Order Integrator with Two Complex Functions Control Parameters for Solving Systems of Initial Value Problems

Authors

  • Opeyemi O. Enoch Department of Mathematics, Federal University Oye-Ekiti, Ekiti State, Nigeria
  • Catherine O. Alakofa Department of Mathematics, Federal University Oye-Ekiti, Ekiti State, Nigeria
  • Lukman O. Salaudeen Department of Mathematics, Federal University Oye-Ekiti, Ekiti State, Nigeria

Keywords:

Numerical integrator, Ordinary di erential equation, Convergence, Consistency

Abstract

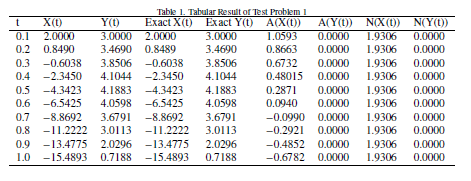
In this study, a numerical integrator that is based on a nonlinear interpolant, for the local representation of the theoretical solution is presented. The resulting integrator aims to solve second and higher-order initial value problems as systems of first-order initial value problems. The method is designed to have two complex functions as control parameters. The control parameters may become real, depending on the nature of the second-order initial value problems to be solved. The generalization and properties of the scheme are also presented.

Dimensions

O. O. Enoch & A. A. Olatunji, “A new self-adjusting numerical integrator for the numerical solutions of ordinary differential equations”, Global Journal GJSFR 12 (2012) 1022.

S. O. Fatunla, “A new algorithm for the numerical solution of ODEs”, Computers and Mathematics with Applications 2 (1976) 247.

J. D. Lambert & B. Shaw, “On the numerical solution of y0 = f (x; y) by a class of formulae based on rational approximations”, Mathematics of Computation 19 (1965) 456.

J. C. Butcher, Numerical Methods for Ordinary Di erential Equation, West Sussex, John Wiley and Sons (2013).

O. O. Enoch & E. A. Ibijola, “A self-adjusting numerical integrator with an inbuilt switch for discontinuous initial value problems”, Australian Journal of Basic and Applied Sciences 5 (2011) 1560.

S. O. Fatunla, Numerical methods for initial value problems in ordinary differential equations, Academic Press, San Diego, U.S.A (1988).

J. D. Lambert, Computational Methods in Ordinary Di erential Systems, John Wiley and Sons, Inc., New York (1973).

J. D. Lambert, Numerical Methods for Ordinary Di erential Systems: the initial value problem, John Wiley and Sons, Inc., New York (1991).

S. E. Fadugba, R. B. Ogunrinde & T. Okunlola, “Eulers method for solving initial value problems in ordinary differential equations”, The Pacific Journal of Science and Technology 13 (2012) 152.

M. A. Islam, “Accurate analysis of numerical solutions of initial value problems (IVP) for ordinary di erential equations (ODE)”, IOSR Journal of Mathematics (IOSR-JM) 11 (2015) 18. http://dx.doi.org/10.5539/jmr.v7n3p41

P. Kama, P. & E. A. Ibijola, “On a new one-step method for numerical solution of ordinary di erential equations”, International Journal of Computer Mathematics 78 (2000) 21.

E. O. Adeyefa & O. S. Esan, “Exponentially fitted Chebyshev based algorithm as second order initial value solver”, Journal of the Nigerian Society of Physical Sciences 2 (2020) 51.

A. O. Anthony, T. Pius, F. A. Onyinyechi & A. D. Ahmed, “Analysis and comparative study of numerical solutions of initial value problems (IVP) in ordinary differential equations (ODE) with Euler and Runge Kutta methods”, American Journal of Engineering Research (AJER) 8 (2019) 40.

S.E. Fadugba, ”Numerical Technique via Interpolating Function for solving Second-order Di erential Equations” Journal of Mathematics and Statistics Research 1(2019) 109.

S. O. Ayinde, A. A., Obayomi & F. S. Adebayo, “Stability analysis of a numerical integrator for solving first order ordinary di erential equation”, Journal of applied Mathematics and Physics 5 (2017) 2196.

S. E. Fadugba & J. O. Idowu, “Analysis of the properties of a third-order convergence numerical method derived via the transcendental function of exponential form”, International Journal of Applied Mathematics and

Theoretical Physics 5 (2019) 97.

M. Humi & W. Miller, “Second course in ordinary di erential equations for scientists and engineers, Springer-Verlag, New York (1988).

H. Ramos, S. Qureshi, A. Soomro ”Adaptive step-size approach for Simpson’s-type block methods with time efficiency and order stars”, Computational and Applied Mathematics 40 (2021) 219.

S. Qureshi, A. Soomro, E. Hincal J. Rye Lee, C. Park & M.S. Osman. ”An efficient variable stepsize rational method for stiff, singular and singularly perturbed problems”, Alexandria Engineering Journal 61 (2022) 12.

S. Qureshi & H. Ramos, ”L-stable explicit nonlinear method with constant and variable step-size formulation for solving initial value problems. International Journal of Nonlinear Sciences and Numerical Simulation,

( 2018) 7.

A. Shokri, ”The Symmetric P-Stable Hybrid Obrenchko Methods for the Numerical Solution of Second Order IVPs”, TWMS J. Pure Appl. Math. 5 (2012) 1.

A. Shokri, H. Saadat & A.R. Khodadadi, A.R., ”A New High Order Closed Newton-Cotes Trigonometrically-fitted Formulae for the Numerical Solution of the Schrodinger Equation”, Iranian Journal of Mathematical Sciences and Informatics 13 (2018) 1.

J. Sunday, C. Chibuisi, E. O. Omole & J. B. Gwong, ”A pair of threestep hybrid block methods for the solutions of linear and nonlinear firstorder systems”, European journal of mathematics and statistics, 3 (2022) 1. https://dx.doi.org/10.24018/ejmath.2022.3.1.86.

A. Ozyapici & T. Karanfiller, ”New integral operator for solution of differential equations”, TWMS J. Pure Appl. Math. 11 (2020) 2.

M. O. Inuejulawo, Development of numerical integrators from a polynomial and rational interpolant for the solution of initial value problem, M.Sc. Thesis, Federal University Oye, Nigeria (2021).

F.T.Krogh, ”A Variable Step Variable Order Multistep Method for the Numerical Solution of Ordinary Di erential Equations” Proc. IFIP Congr. (1968).

S. E. Fadugba & B. O. Falodun, “Development of a new one-step scheme for the solution of initial value problem (IVP) in ordinary differential equations”, International Journal of Theoretical and Applied Mathematics 3 (2017) 58.

S. E. Fadugba, S.N. Ogunyebi & B. O. Falodun, “An examination of a second order numerical method for solving initial value problems”, Journal of the Nigerian Society of Physical Sciences 2 (2020) 120. https://doi.org/10.46481/jnsps.2020.92.

P. Henrici, Discrete Variable Methods in ODE, JohnWiley and Sons, Inc., New York (1962).

E. A. Ibijola, O. O. Bamisile & J. Sunday, “On the derivation and applications of a new one-step method based on the combination of two interpolating functions”, American Journal of Scientific and Industrial Research 2 (2011) 422.

M. A. Islam, “Accurate solutions of initial value problems for ordinary differential equations with the fourth order Runge Kutta method”, Journal of Mathematics Research 7 (2015) 41.

J. O. Kuboye, O. F. Quadri & O. R. Elusakin, “Solving Third order Differential Equation directly using hybrids Numerical medels”, Journal of the Nigerian Society of Physical Sciences 2 (2020) 69. https://doi.org/10.46481/jnsps.2020.43

A. A. Qalandarov & A. A. Khaldjigitov, “Mathematical and numerical modeling of the coupled dynamic thermoelastic problems for isotropic bodies”, TWMS J. Pure Appl. Math. 11 (2020) 1.

Published

2022-12-16

How to Cite

Odd Order Integrator with Two Complex Functions Control Parameters for Solving Systems of Initial Value Problems. (2022). Journal of the Nigerian Society of Physical Sciences, 5(1), 968. https://doi.org/10.46481/jnsps.2023.968

Issue

Volume 5, Issue 1, February 2023

Section

Original Research
Copyright & Licensing

Copyright (c) 2022 Opeyemi O. Enoch, Catherine O. Alakofa , Lukman O. Salaudeen

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Odd Order Integrator with Two Complex Functions Control Parameters for Solving Systems of Initial Value Problems. (2022). Journal of the Nigerian Society of Physical Sciences, 5(1), 968. https://doi.org/10.46481/jnsps.2023.968