Collocation Method for the Numerical Solution of Multi-Order Fractional Differential Equations

Authors

  • G. Ajileye Department of Mathematics and Statistics, Federal University Wukari, Taraba State, Nigeria
  • A. A. James Department of Mathematics and Statistics, American University of Nigeria, Yola, Adamawa State, Nigeria.

Keywords:

Differential equation, Fractional derivatives, Approximate solution, Power series

Abstract

This study presents a collocation approach for the numerical integration of multi-order fractional differential equations with initial conditions in the Caputo sense. The problem was transformed from its integral form into a system of linear algebraic equations. Using matrix inversion, the algebraic equations are solved and their solutions are substituted into the approximate equation to give the numerical results. The effectiveness and precision of the method were illustrated with the use of numerical examples.

Dimensions

S.Abbas, & D.Mehdi, “A new operational matrix for solving fractional order differential equations”, Computer and Mathematics with Application 59 (2010) 1326, doi:10.1016/j.camwa.2009.07.006.

O. A. Uwaheren, A. F. Adebisi & O. A. Taiwo, “Perturbed Collocation Method For Solving Singular Multi-order Fractional Differential Equations of Lane-Emden Type”, Journal of the Nigerian Society of Physical Sciences 3 (2020) 141, https://doi.org/10.46481/jnsps.2020.69.

A. M. Wazwaz & S. M. El-Sayed, “A new modification of the Adomian decompostion method for linear and nonlinear operators”, App. Math. Comput. 122 (2001) 393.

R. H. Khan & H. O. Bakodah, “Adomian decomposition method and its modification for nonlinear Abel’s integral equations”, Computers and Mathematics with Applications 7 (2013) 2349.

R. C. Mittal & R. Nigam. ”Solution of fractional integro-differential equations by Adomiandecomposition method”, The International Journal of Applied Mathematics and Mechanics 2 (2008) 87.

D. A. Gegele, O. P. Evans & D. Akoh, “Numerical solution of higher order linear Fredholm integro-differential equations”, American Journal of Engineering Research 3 (2014) 243.

O. A. Agbolade & T. A. Anake, “Solutions of first-order Volterra type linear integro differential equations by collocation method”, Journal of Applied Mathematics 4 (2017) 1. doi: 10.1155/2017/1510267.

S. Nemati, P. Lima & Y. Ordokhani, “Numerical method for the mixed Volterra-Fredholm integral equations using hybrid Legendre function”, Conference Application of Mathematics 4 (2015) 184.

A. O. Adesanya, Y. A.Yahaya, B. Ahmed & R. O. Onsachi, “Numerical Solution of Linear integral and Integro-Differential Equations Using Boubakar Collocation Method”, International Journal of Mathematical Analysis and Optimization: Theory and Application 2 (2019) 592.

K. Issa & F. Saleh, “Approximate solution of pertubed Volterra Fredholm integro differential equation by Chebyshev-Galerkin method”, Journal of Mathematics 17 (2017) 6. doi:10,1155/2017/8213932.

A. H. Bhraway, E. Tohidi & F. Soleymani, “A new Bernoulli matrix method for solving high order linear and nonlinear Fredholm integro-differential equations with piecewise interval”, Appl. Math. Comput. 219(2012) 482.

C. Ercan & T. Kharerah, “Solving a class of Volterra integral system by the differential transform method”, Int. J. Nonlinear Sci. 16 (2013) 87.

M. El-kady & M. Biomy, “Efficient Legendre pseudospectral method for solving integral and integro differential equation”, Commom Nonlinear Sci. Numer. Simulat. 15 (2010) 1724.

N. Irfan, S. Kumar & S. Kapoor, “Bernstein Operational Matrix Approach for Integro-Differential Equation Arising in Control theory ”, Nonlinear Engineering 3 (2014) 117.

M. K. Shahooth, R. R. Ahmed, U-K. S. Din, W. Swidan, O. K. Al-Husseini & W. K. Shahooth, “Approximation Solution to Solving Linear Volterra-Fredholm Integro-Differential Equations of the Second Kind by Using Bernstein Polynomials Method”, J. Appl. Computat. Math. 5 (2016) 228, DOI:10.4172/2168-9679.1000298.

S. E. Fadugba, “Solution of Fractional Order Equations in the Domain of the Mellin Transform”, Journal of the Nigerian Society of Physical Sciences 4 (2019) 138, https://doi.org/10.46481/jnsps.2019.31.

A. Bolandtalat, E. Babolian, H. Jafari, “Numerical solution of multi-order fractional differential equations by Boubakar polynomial”, Open Phys 14 (2016) 226.

G. Ajileye, A. A. James, A. M. Ayinde & T. Oyedepo, “Collocation Approach for the Computational Solution Of Fredholm-Volterra Fractional Order of Integro-Differential Equations”, J. Nig. Soc. Phys. Sci. 4 (2022) 834.

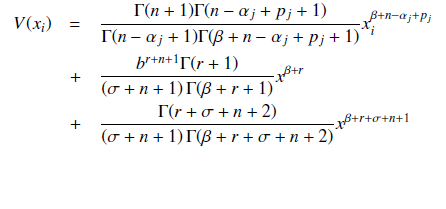
Published

2023-06-11

How to Cite

Collocation Method for the Numerical Solution of Multi-Order Fractional Differential Equations. (2023). Journal of the Nigerian Society of Physical Sciences, 5(3), 1075. https://doi.org/10.46481/jnsps.2023.1075

Issue

Volume 5, Issue 3, August 2023

Section

Original Research
Copyright & Licensing

Copyright (c) 2023 G. Ajileye, A. A. James

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Collocation Method for the Numerical Solution of Multi-Order Fractional Differential Equations. (2023). Journal of the Nigerian Society of Physical Sciences, 5(3), 1075. https://doi.org/10.46481/jnsps.2023.1075