Numerical Solution of Second Order Fuzzy Ordinary Differential Equations using Two-Step Block Method with Third and Fourth Derivatives
Keywords:
Fuzzy initial value problem, Fuzzy boundary value problem, Second order, Two-step, Block method, Linear, NonlinearAbstract
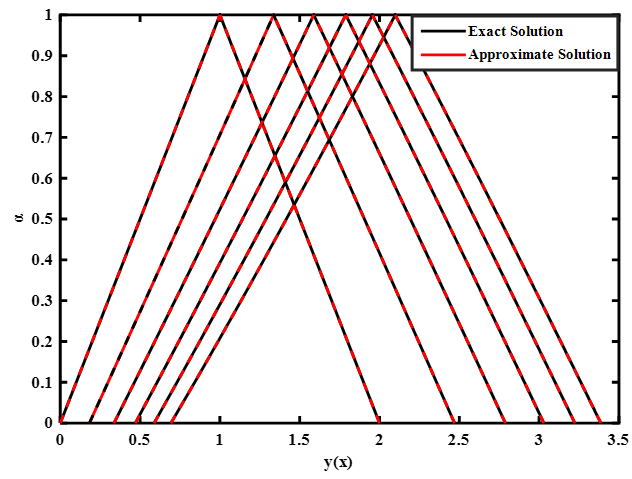
Fuzzy differential equation models are suitable where uncertainty exists for real-world phenomena. Numerical techniques are used to provide an approximate solution to these models in the absence of an exact solution. However, existing studies that have developed numerical techniques for solving second-order fuzzy ordinary differential equations (FODEs) possess an absolute error accuracy that could be improved. Therefore, this article developed a more accurate higher derivative self-starting block scheme for the numerical solution of second-order FODEs with fuzzy initial and boundary conditions imposed. Linear block approach using Taylor series expansion is adopted for the derivation of the proposed method and the basic properties are established using the definitions of stability and consistency for block methods. According to the numerical results, when compared to the exact solution in terms of absolute error, the new method proposed in this article outperformed existing numerical methods. It is thus concluded that the proposed method is effective for solving second-order FODEs directly.
Published
How to Cite
Issue
Section
Copyright (c) 2023 Kashif Hussain, Oluwaseun Adeyeye, Nazihah Ahmad

This work is licensed under a Creative Commons Attribution 4.0 International License.






