Typhoid fever dynamical model with cost-effective optimalcontrol
Keywords:
Cost-effectiveness analysis, global sensitivity analysis, optimal control analysis, typhoid feverAbstract
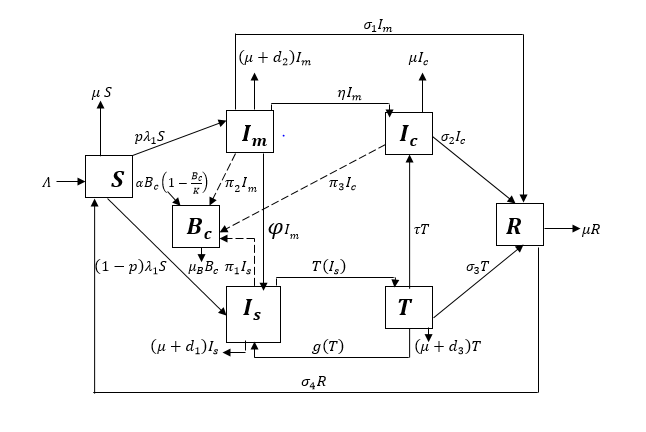
Typhoid fever is a highly communicable and infectious disease that can be fatal and causes severe complications if unattended to timely. The infection, at times, can be more complex, challenging, and impossible to treat as antibiotics become less effective. Hence, the effect of limited clinical efficacy of the antibiotics with corresponding relapse response to treatment on infected humans is considered in this paper by formulating a deterministic model for direct and indirect transmission mode of Typhoid infection. The basic reproduction number is analytically derived and used to implement the global sensitivity analysis. Following the sensitivity analysis result, the optimal control analysis is carried out and simulated numerically with four controls: sanitation and hygiene practice and awareness campaign control, sterilisation and disinfection control, the potency of antibiotics control and screening control. Finally, the cost-effectiveness analysis for infected and susceptible humans with four cases that compared fifteen strategies is analysed. The results indicate that the sanitation and hygiene practice and awareness campaign is good to implement for single control implementation, while for double control implementation, Strategy 6, which is the combination of Strategy 1 and the potency of antibiotics administered to typhoid patients, is the best to consider. Combining Strategy 6 and screening control is the most cost-effective for triple controls. Furthermore, the overall computation of cost-effectiveness among all the most cost-effective with all the controls combined suggests that sanitation and hygiene practice and awareness campaign is the most cost-effective strategy to implement for eradicating typhoid infection in the population and for preventing susceptible populations from contracting the bacteria.
Published
How to Cite
Issue
Section
Copyright (c) 2023 Chinwendu E. Madubueze, Kazeem A. Tijani, Reuben I. Gweryina

This work is licensed under a Creative Commons Attribution 4.0 International License.






