Analysis of a fractional order climate model due to excessive emission and accumulation of carbon dioxide in the atmosphere
Keywords:
Climate change, Fractional order, Carbon dioxide, Excessive emissionAbstract
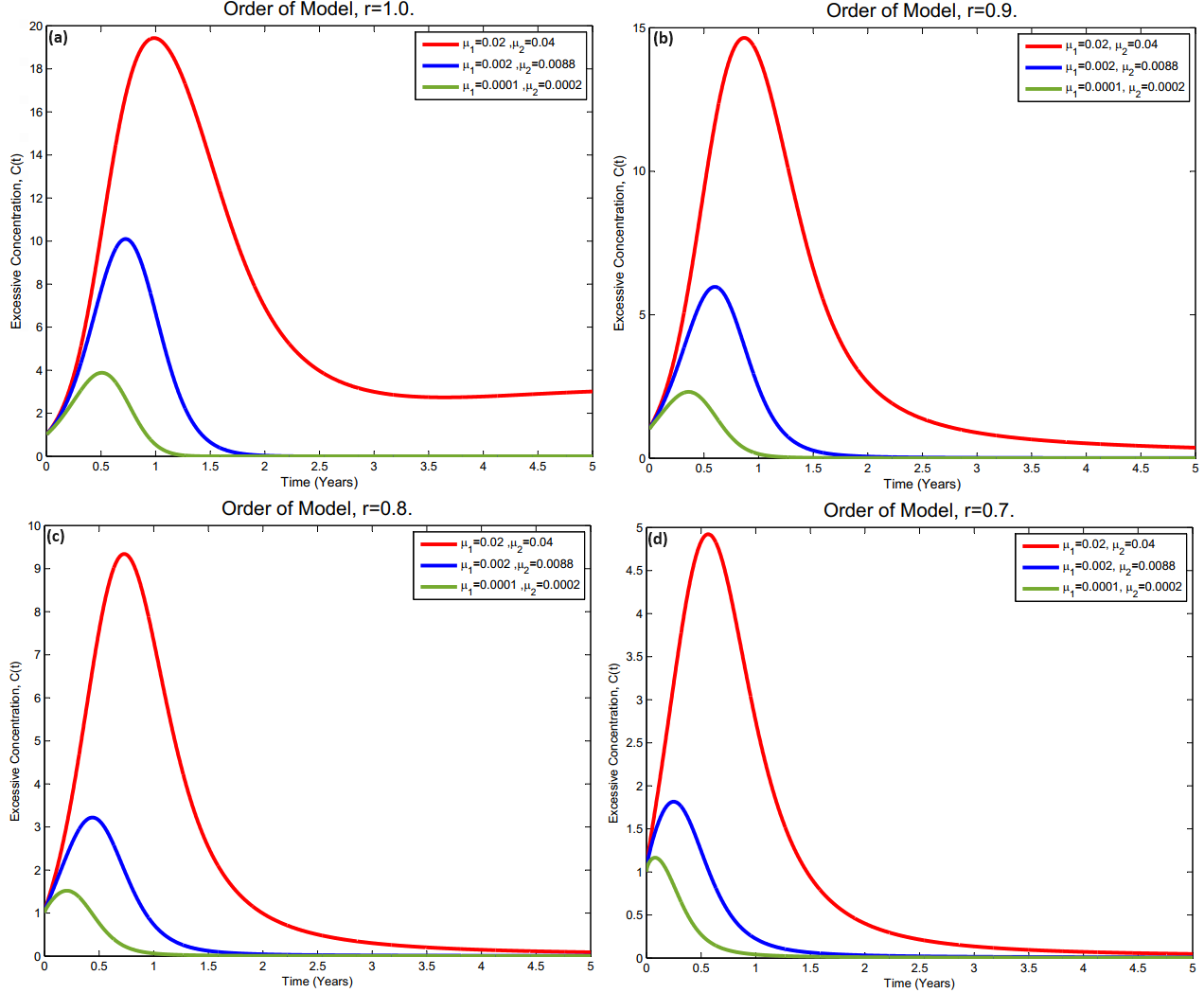
The devastating consequences of climate change on our planet cannot be taken lightly. Greenhouse gas emissions due to the various activities of the increasing human population are solely responsible for this change. The chief and most significant of these gases is carbon dioxide. A fractional-order model of five compartments is considered. The uniqueness and existence, the positivity, and the boundedness of the model solution are established. The equilibrium points of the model are given. By formulating different Lyapunov functions, the global stability of the four equilibrium points was determined. The numerical simulation of the model was done using the Predict-Evaluate-Correct-Evaluate method of Adam-Bashforth-Moulton by considering four different orders of 0.7, 0.8, 0.9, and 1.0. According to the results, excessive concentrations of carbon dioxide in the atmosphere can be reduced by the joint employment of mitigation measures.
Published
How to Cite
Issue
Section
Copyright (c) 2023 Peter Urane Achimugwu, Mathew Ngugi Kinyanjui, David Mumo Malonza

This work is licensed under a Creative Commons Attribution 4.0 International License.






