Entropic system in the relativistic Klein-Gordon Particle
Keywords:
Eigensolutions, Bound states, Wave equation, Theoretic quantityAbstract
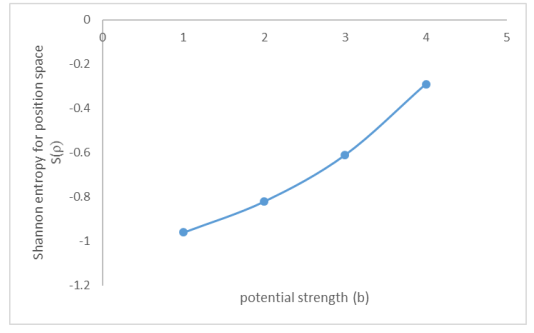
The solutions of Kratzer potential plus Hellmann potential was obtained under the Klein-Gordon equation via the parametric Nikiforov-Uvarov method. The relativistic energy and its corresponding normalized wave functions were fully calculated. The theoretic quantities in terms of the entropic system under the relativistic Klein-Gordon equation (a spinless particle) for a Kratzer-Hellmann’s potential model were studied. The effects of a and b respectively (the parameters in the potential that determine the strength of the potential) on each of the entropy were fully examined. The maximum point of stability of a system under the three entropies was determined at the point of intersection between two formulated expressions plotted against a as one of the parameters in the potential. Finally, the popular Shannon entropy uncertainty relation known as Bialynick-Birula, Mycielski inequality was deduced by generating numerical results.
Published
How to Cite
Issue
Section
Copyright (c) 2021 Journal of the Nigerian Society of Physical Sciences

This work is licensed under a Creative Commons Attribution 4.0 International License.






