Discretization of the Caputo time-fractional advection-diffusion problems with certain wavelet basis function
Keywords:
Caputo fractional derivatives, Time-fractional advection-diffusion equations (TFADE), Iweobodo-Mamadu-Njoseh wavelet (IMNW), Time discretization, Space discretizationAbstract
Considering the new wavelet-based Galerkin finite element technique constructed with Iweobodo-Mamadu-Njoseh wavelet (IMNW) as the basis function in seeking the numerical solution of time-fractional advection-diffusion equations (TFADE), the TFADE must be simplified to enhance an application of a numerical technique. Thus in this research work, we considered an implementation of the time and space discretization of the TFADE with the
use of IMNW basis function. In order to successfully achieve our result, our methodology inculcated the Caputo fractional derivatives, time fractional advection-diffusion equations (TFADE), Wavelet, IMNW, and Galerkin finite element method. After a successful implementation of the time discretization, an implicit form of TFADE was obtained, followed by the implementation of the space discretization which generated the variational formulation of the equation for easy implementation of the scheme. The illustrated numerical solution from using the new technique provided a resulting numerical evidence which aligns with the exact solution.
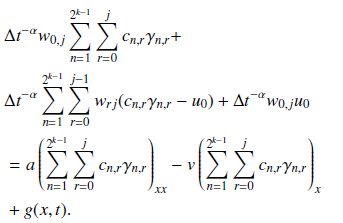
Published
How to Cite
Issue
Section
Copyright (c) 2025 D. C. Iweobodo, G. C. Abanum, O. Ogoegbulem , N. I. Ochonogor, I. N. Njoseh

This work is licensed under a Creative Commons Attribution 4.0 International License.






