Machine learning-based feature selection for ultra-high-dimensional survival data: a computational approach
Keywords:
Ultra-high dimension, Machine Learning, Feature Selection, Renal Cell Carcinoma, Survival DataAbstract
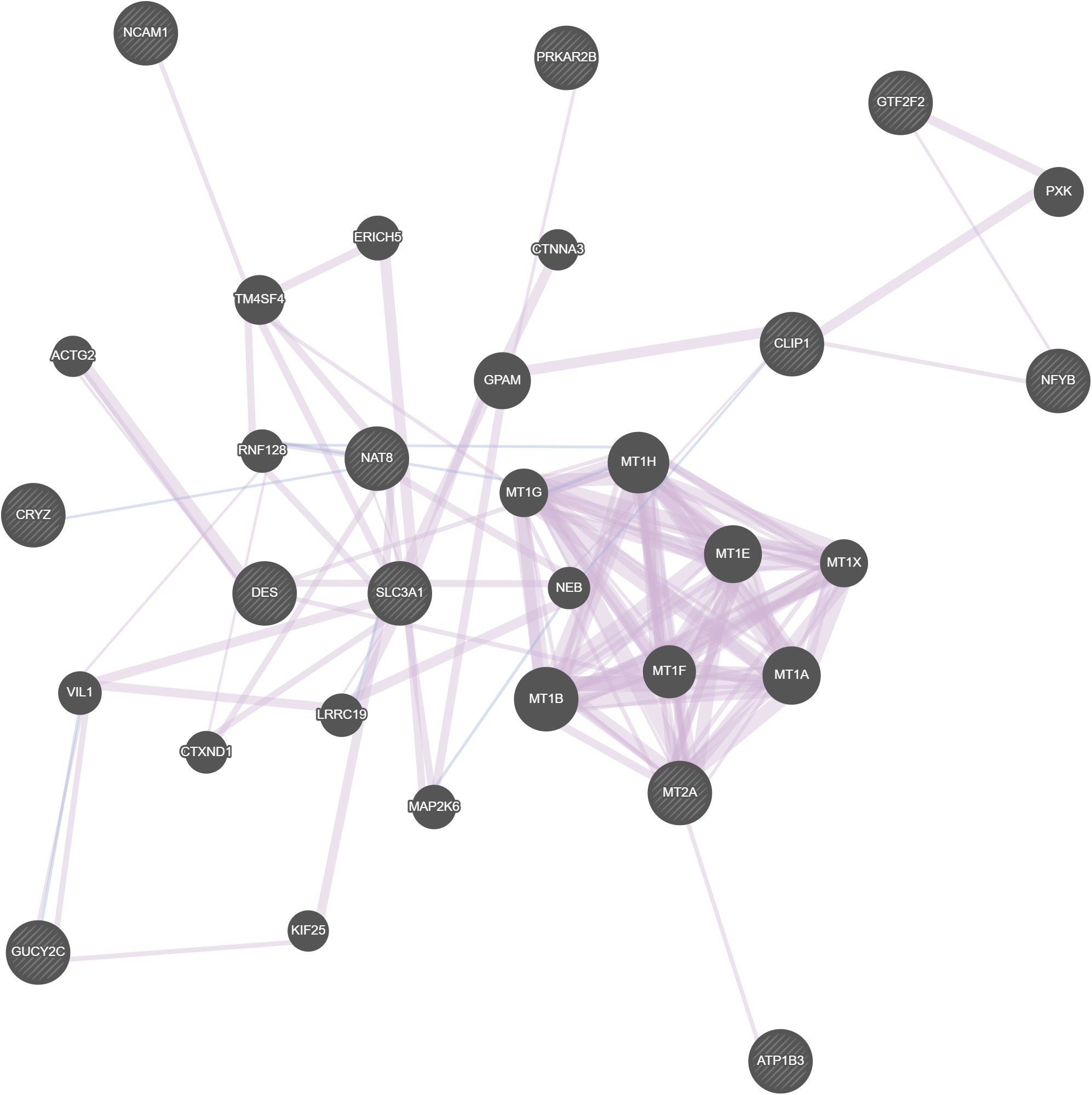
Ultra-high-dimensional (UHD) survival data presents significant computational challenges in biomedical research, particularly in Renal Cell Carcinoma (RCC), where genomic complexity complicates risk assessment. Effective feature selection is crucial for identifying key biomarkers that improve RCC diagnosis, prognosis, and treatment. This study evaluates machine learning (ML)-based feature selection methods to address limitations in scalability, feature redundancy, and predictive accuracy in UHD RCC survival data. Gene expression data from 4,224 differentially expressed genes across 74 individuals was analyzed using LASSO, EN, Adaptive LASSO, Group LASSO, SIS, ISIS, SCAD, and SVM. Models were assessed using Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and R² values. SCAD demonstrated the best predictive performance (MSE: 529.00, RMSE: 23.00, R²: 0.69), surpassing ISIS (R²: 0.61), SIS (R²: 0.60), and EN (R²: 0.57). LASSO and Adaptive LASSO underperformed. SCAD identified 14 key genes—NCAM1, ATP1B3, NAT8, MT2A, GTF2F2, X4197, GUCY2C, SLC3A1, CRYZ, DES, MT1L, NFYB, PRKAR2B, and CLIP1—as potential RCC biomarkers. Gene interaction network analysis confirmed their role in RCC progression. Despite SCAD’s strong performance, it left 31% of data variability unexplained, suggesting hybrid ML models that integrate ensemble learning, two-component regression structures, and deep learning-based feature selection could further enhance gene selection and predictive accuracy. This research supports SDG 3 (Good Health and Well-being) and SDG 9 (Industry, Innovation, and Infrastructure) by advancing precision medicine, early RCC detection, and biomedical data-driven innovations for improved clinical decision-making.
Published
How to Cite
Issue
Section
Copyright (c) 2025 Nahid Salma, Majid Khan Majahar Ali, Raja Aqib Shamim

This work is licensed under a Creative Commons Attribution 4.0 International License.






