Evaluating feature selection methods in a hybrid Weibull Freund-Cox proportional hazards model for renal cell carcinoma

Shaymaa Mohammed Ahmed; Majid Khan  Majahar Ali; Arshad Hameed  Hasan

doi:10.46481/jnsps.2025.2812

Authors

Shaymaa Mohammed Ahmed
[email protected]
School of Mathematical Sciences; University Sains Malaysia, 11800 USM, Penang
Majid Khan Majahar Ali School of Mathematical Sciences; University Sains Malaysia, 11800 USM, Penang
Arshad Hameed Hasan College of Administration and Economics; University of Diyala, 32001, Diyala,Iraq

Keywords:

Renal Cell Carcinoma (RCC), Weibull-Freund-Cox Proportional Hazards Model, Feature selection, Lasso regression, MI-SVM

Abstract

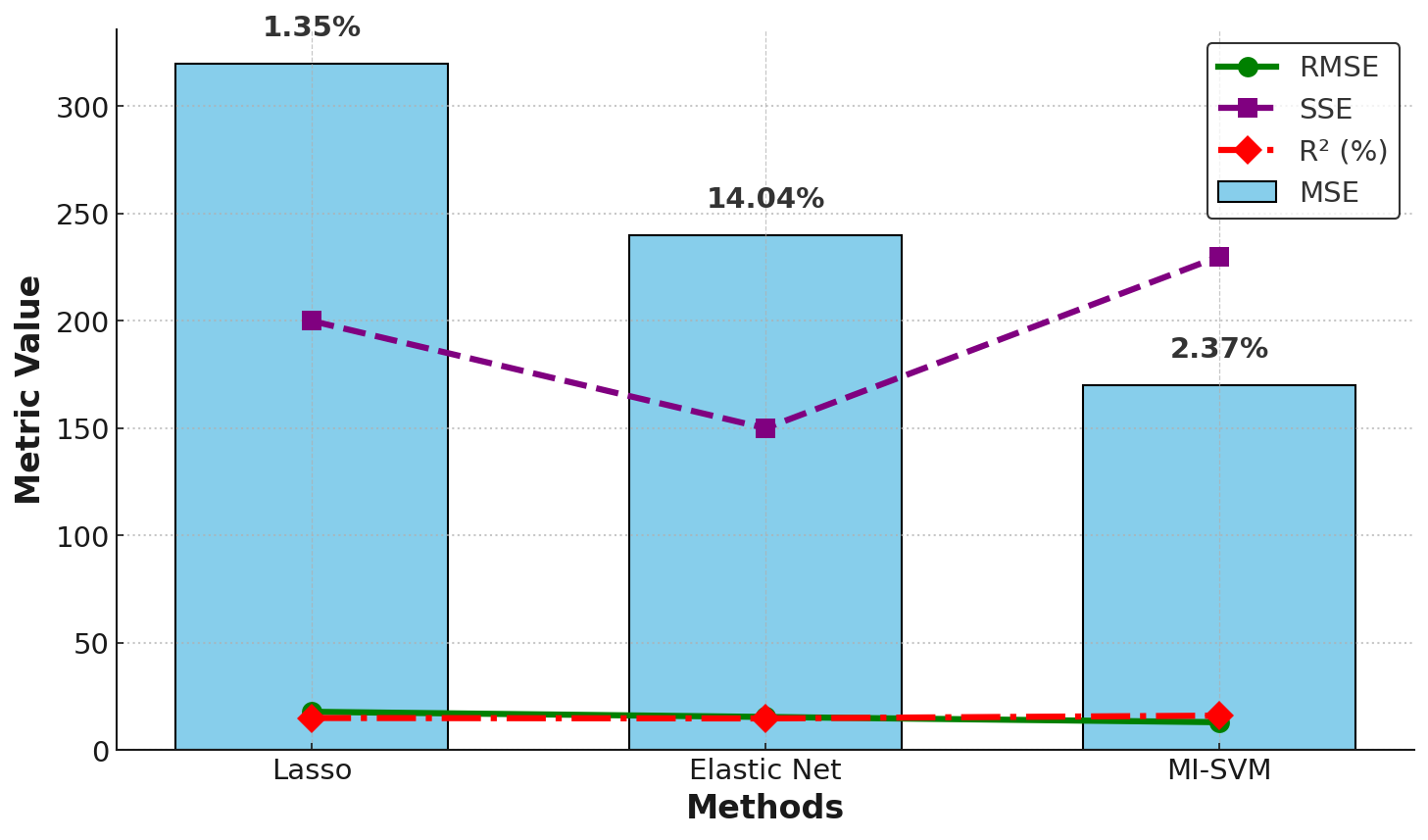
This paper reports a feature selection comparison between Lasso, Elastic Net, and Mutual Information-Support Vector Machine (MI-SVM) that are based on a hybrid Weibull-Freund-Cox Proportional Hazards (WFCPH) model when it is used with renal cell carcinoma (RCC) data. The purpose is to determine which genes are dominant in RCC and evaluate the degree of efficiency of each method. Lasso, which performs rigorous selection for features, obtained quite a small set of genes, and the advantage was made in the simplicity and interpretability of the classifier. Still, the models had the lowest predictive ability. Elastic Net ‘averted’ some difficulties of Lasso combined with Ridge regression and selected more or less different genes for better fitting of the model. MI-SVM was the optimal procedure for this task, considering the number of features chosen and the performances obtained, with the highest R2 and the lowest MSE. The study provides valuable information on which approach to use in survival analysis using the WFCPH model by contrasting the advantages and disadvantages of each approach covered.

Dimensions

REFERENCES

[1] G. N. Bekiroglu, E. Avci & E. G. Ozgur, “What is the best method for long-term survival analysis?”, Indian Journal of Cancer 59 (2022) 457. https://doi.org/10.4103/ijc.IJC_22_21.

[2] A. Begun & E. Kulinskaya, “A simulation study of the estimation quality in the double-Cox model with shared frailty for non-proportional hazards survival analysis”, arXiv, 2022. [Online]. https://doi.org/10.48550/arXiv.2206.05141.

[3] M. Cooper, R. Greiner & R. G. Krishnan, “Copula-based deep survival models for dependent censoring”, arXiv, 2023. [Online]. https://doi.org/10.48550/arXiv.2306.11912.

[4] A. H. Kamal, M. H. M. Janssen, L. A. Lacasse, W. L. Dahut & J. E. Bekelman, “The future of cancer care at home: findings from an American Cancer Society summit”, CA: A Cancer Journal for Clinicians 73 (2023) 353. https://doi.org/10.3322/caac.21784.

[5] Z. Wang & Y. Zhang, “Hybrid Weibull reliability modeling of ATC system based on graphical method and genetic algorithm”, Proceedings of SPIE (2023). https://doi.org/10.1117/12.3011822.

[6] M. P. Bhatt, S. B. Heller, M. Kapustin, M. Bertrand & C. Blattman, “Predicting and preventing gun violence: an experimental evaluation of READI Chicago”, The Quarterly Journal of Economics 139 (2023) 1. https://doi.org/10.1093/qje/qjad031.

[7] N. Bett, J. Kasozi & D. Ruturwa, “Dependency modeling approach of cause-related mortality and longevity risks: HIV/AIDS”, Risks 11 (2023). https://doi.org/10.3390/risks11020038.

[8] K. Finlay, M. Mueller-Smith & B. Street, “Children?s indirect exposure to the U.S. justice system: evidence from longitudinal links between survey and administrative data”, The Quarterly Journal of Economics 138 (2023) 2181. https://doi.org/10.1093/qje/qjad021.

[9] M. Fillon, “Near majority of adults favor R ratings for films with smoking”, CA: A Cancer Journal for Clinicians 73 (2023) 118. https://doi.org/10.3322/caac.21776.

[10] G. Mulugeta, T. Zewotir, A. S. Tegegne, L. H. Juhar & M. Bekele, “Developing clinical prognostic models to predict graft survival after renal transplantation: comparison of statistical and machine learning models”, Research Square (2024). [Online]. https://doi.org/10.21203/rs.3.rs-4128455/v1.

[11] H. Lee, C. Chen, P. Kochunov, L. E. Hong & S. Chen, “Modeling multivariate age-related imaging variables with dependencies”, Statistics in Medicine 41 (2022) 4484. https://doi.org/10.1002/sim.9522.

[12] A. H. Al-Rammahi & T. R. Dikheel, “Freund?s model with iterated sure independence screening in Cox proportional hazard model”, AIP Conf. Proc. 2398 (2022) 060009. https://doi.org/10.1063/5.0093464.

[13] N. V. Kuznietsova, V. H. Huskova, P. I. Bidyuk, Y. Matsuki & L. B. Levenchuk, “Modeling risk factors interaction and risk estimation with copulas”, Radio Electronics, Computer Science, Control 2 (2022). https://doi.org/10.15588/1607-3274-2022-2-5.

[14] H. H. Huang & Y. Liang, “A novel Cox proportional hazards model for high-dimensional genomic data in cancer prognosis”, IEEE/ACM Transactions on Computational Biology and Bioinformatics 80 (2023) 1821. https://doi.org/10.1109/TCBB.2019.2961667.

[15] W. Huber, R. Wagner & H. Sueltmann, “Transcription profiling of 74 kidney tumor samples of different histological type, differentiation grade, stage and with data on chromosomal aberrations and follow-up”, BioStudies, E-DKFZ-1, 2013. [Online]. https://www.ebi.ac.uk/biostudies/arrayexpress/studies/E-DKFZ-1.

[16] J. Wang, D. Zeng & D. Y. Lin, “Fitting the Cox proportional hazards model to big data”, Biometrics 80 (2024) ujae018. https://doi.org/10.1093/biomtc/ujae018.

[17] H. Rehman, N. Chandra & A. H. Abuzaid, “Analysis and modelling of competing risks survival data using modified Weibull additive hazards regression approach”, Hacettepe Journal of Mathematics and Statistics 52 (2023) 1263. https://doi.org/10.15672/hujms.1066111.

[18] L. P. Chen, “Analysis of length-biased and partly interval-censored survival data with mismeasured covariates”, Biometrics 79 (2023) 3929. https://doi.org/10.1111/biom.13898.

[19] Z. Ning, Z. Lin, Q. Xiao, D. Du, Q. Feng, W. Chen, Y. Zhang, “Multi-constraint latent representation learning for prognosis analysis using multi-modal data”, IEEE Transactions on Neural Networks and Learning Systems 34 (2023) 3737. https://doi.org/10.1109/TNNLS.2021.3112194.

[20] B. Guo & N. Yi, “A scalable and flexible Cox proportional hazards model for high-dimensional survival prediction and functional selection”, arXiv, 2022. [Online]. https://arxiv.org/abs/2205.11600.

[21] A. Begun, E. Kulinskaya & N. Ncube, “A double-Cox model for non-proportional hazards survival analysis with frailty”, Statistics in Medicine 42 (2023) 3114. https://doi.org/10.1002/sim.9760.

[22] A. Arora, C. Sehgal & N. Agarwal, “An analysis of machine learning algorithms for chronic kidney disease prediction”, 14th International Conference on Cloud Computing, Data Science & Engineering (Confluence), Noida, India, 2024, pp. 581-586. https://doi.org/10.1109/confluence60223.2024.10463505.

[23] R. K. Halder, M. N. Uddin, Md. A. Uddin, S. Aryal, S. Saha, R. Hossen, S. Ahmed, M. A. Rony, M. F. Akter, “ML-CKDP: machine learning-based chronic kidney disease prediction with smart web application”, Journal of Pathology Informatics 15 (2024) 100371. https://doi.org/10.1016/j.jpi.2024.100371.

[24] M. Abdulkabir, A. A. Oshioke, U. A. Edem & R. S. Tunde, “Gradient curve of Cox proportional hazard and Weibull models”, Journal of Biometrics and Biostatistics 2 (2017) 1. https://doi.org/10.4172/2090-5092.1000108.

[25] B. C. Kim, “Dependence modeling for large-scale project cost and time risk assessment: additive risk factor approaches”, IEEE Transactions on Engineering Management 70 (2023) 417. https://doi.org/10.1109/TEM.2020.3046542.

[26] M. Ellahi, G. Abbas, H. F. Usman & M. A. S. Hassan, “Comparative analysis of Weibull parameter estimation using HPSOBA and standard PSO and classical bat algorithms”, International Journal of Science, Engineering and Technology 1 (2022) 1. https://doi.org/10.56536/ijset.v2i1.10.

[27] N. Nurhayati, A. W. Bustan, M. Salmin & T. Talib, “Perbandingan model regresi Weibull dan regresi Cox proposional hazard”, Science Map Journal 4 (2022) 49. https://doi.org/10.30598/jmsvol4issue2pp49-60.

[28] C. Ai & S. Shi, “The square-root elastic net with a new calculating method”, Highlights in Science, Engineering and Technology 49 (2023) 470. https://doi.org/10.54097/hset.v49i.8597.

[29] K. Omae & S. Eguchi, “Quasi-linear Cox proportional hazards model with cross-L1 penalty”, BMC Medical Research Methodology 20 (2020) 182. https://doi.org/10.1186/S12874-020-01063-2.

[30] M. Sajjia, S. Shirazian, D. Egan, J. Iqbal, A. B. Albadarin, M. Southern, G. Walker, “Mechanistic modelling of industrial-scale roller compactor ?Freund TF-MINI model?”, Computers and Chemical Engineering 104 (2017) 141. https://doi.org/10.1016/j.compchemeng.2017.04.018.

[31] Y. Hasija & R. Chakraborty, “Support vector machines”, in Artificial Intelligence: Theories and Applications, R. K. Choudhary (Ed.), CRC Press, Boca Raton, USA, 2021, pp. 215–232. https://doi.org/10.1201/9781003090113-12-12.

[32] M. Franco, J. M. Vivo & D. Kundu, “A generalized Freund bivariate model for a two-component load sharing system”, Reliability Engineering & System Safety 203 (2020) 107096. https://doi.org/10.1016/j.ress.2020.107096.

[33] S. Chen & F. Yang, “Expectation-maximization algorithm for the Weibull proportional hazard model under current status data”, Mathematics 11 (2023) 4826. https://doi.org/10.3390/math11234826.

[34] F. Hamad & N. N. Kachouie, “A hybrid method to estimate the full parametric hazard model”, Communications in Statistics - Theory and Methods 48 (2019) 5477. https://doi.org/10.1080/03610926.2018.1513149.

[35] K. K. Mahanta & J. Hazarika, “A multivariate proportional odds frailty model with Weibull hazard under Bayesian mechanism”, Indian Journal of Science and Technology 16 (2023) 30. http://dx.doi.org/10.17485/IJST/v16iSP2.6447.

[36] K. Xu, L. Han, Y. Tian, S. Yang & X. Zhang, “EQ-Net: elastic quantization neural networks”, arXiv, 2023. [Online]. https://doi.org/10.48550/arxiv.2308.07650.