An analytical model for point source pollutants  in an urban area with mesoscale wind and wet deposition

Authors

  • R. Latha Department of Mathematics, Jyothy Institute of Technology, CIIRC, Bengaluru 560085, India | Visvesvaraya Technological University, Belagavi 590018, India.
  • K. Lakshminarayanachari Visvesvaraya Technological University, Belagavi 590018, India. | Department of Mathematics, Sai Vidya Institute of Technology, Bengaluru 560064, India.
  • C. Bhaskar Visvesvaraya Technological University, Belagavi 590018, India. | Department of Mathematics, Sai Vidya Institute of Technology, Bengaluru 560064, India.

Keywords:

Urban heat island, Dry deposition, Advection-diffusion equation, Wet deposition, Atmospheric impurities

Abstract

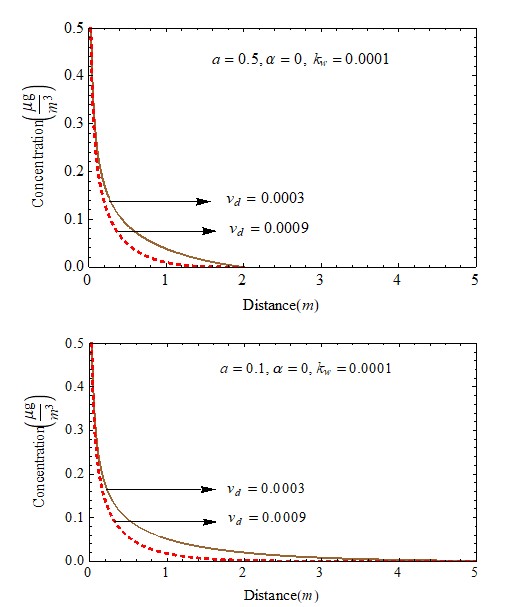
Industrialization has led to severe environmental degradation, posing substantial health risks. The primary pollutants originate from land, air, and water sources. Monitoring air pollution typically requires expensive equipment. To address this, scientists have created various models based on specific criteria to predict air pollution levels. This paper explores an analytical solution to the problem of air pollution caused by point sources that disperse contaminants into the atmosphere. Specifically, it investigates how the removal processes affect the concentration of key pollutants. We apply the methods of separation of variables and Fourier transformation to derive an analytical solution for the mathematical model.

Dimensions

F. Pasquil & F. B. Smith, Atmospheric diffusion (3rd Edition), Ellis Horwood Ltd., Chichester, England, 1983, pp 437. https://doi.org/10.1002/qj.49711046416.

J. S. Lin & L. M. Hildemann, “Analytical solutions of the atmospheric diffusion equation with multiple sources and height-dependent wind speed and eddy diffusivities”, Atmospheric Environment, 30 (1996) 239. https://doi.org/10.1016/1352-310(95)00287-9

K. S. M. Essa, A. S. Shalaby, M. A. E. Ibrahim et al., “Analytical solutions of the advection-diffusion equation with variable vertical eddy diffusivity and wind speed using Hankel transform”, Pure Appl. Geophys. 177 (2020) 4545. https://doi.org/10.1007/s00024-020-02496-y.

M. Sharan & M. Modani, “An analytical study for the dispersion of pollutants in a finite Layer under Low Wind Conditions”’, Pure Appl. Geophy. 162 (2005) 1861. https://doi.org/10.1007/s00024-005-2696-5.

A. A. Marrouf, K. S. M. Essa, M. S. El-Otaify1, A. S. Mohamed & G. Ismail, “The influence of eddy diffusivity variation on the atmospheric diffusion equation”, Open Journal of Air Pollution 04 (2015) 109. http://dx.doi.org/10.4236/ojap.2015.43011.

K. Pramod & S. Maithili, “An analytical model for dispersion of pollutants from a continuous source in the atmospheric boundary layer”, Proc. R. Soc. A. 466 (2010) 383. https://doi.org/10.1098/rspa.2009.0394.

J. F. Dilley & K. T. Yen, “Effect of a mesoscale type wind on the pollutant distribution from a line source”, Atmospheric Environment 5 (1971) 843. https://doi.org/10.1016/0004-981(71)90014-X.

U. Arora, S. Gakkhar & R. S. Gupta, “Removal model suitable for air pollutants emitted from an elevated source”, Applied Mathematical Modelling 15 (1991) 386. https://doi.org/10.1016/0307-4X(91)90065-W.

D. Buske, “An analytical solution of the advection-diffusion equation considering non-local turbulence closure", Environ Fluid Mech 7 (2007) 43. https://doi.org/10.1007/s10652-006-9012-5.

Y. S. Park & J. J. Baik, “Analytical solution of the advection-diffusion equation for a ground-level finite area source”, Atmospheric Environment 42 (2008) 9063. https://doi.org/10.1016/j.atmosenv.2008.09.019.

K. Lakshminarayanachari, K. L. Sudheer Pai,M.Siddalinga prasad, C. Pandurangappa, “A two-dimensional numerical model of primary pollutant emitted from an urban area source with mesoscale wind, dry deposition and chemical reaction”, Atmospheric Pollution Research 4 (2013) 106. https://doi.org/10.5094/APR.2013.011.

E. Khaled, S. Sawsan, W. Ali & E. N. Mostafa, “Studying the effect of the instantaneous and continuous pollutants sources on the advection-diffusion equation and its Applications”, Iraqi Journal of Science 65 (2024) 1117. https://doi.org/10.24996/ijs.2024.65.2.41.

C. Bhaskar, K. Lakshminarayanachari & C. Pandurangappa, “Analytical Approach for Air pollution Emitted from Line source with Chemical reaction and wet deposition”, International Journal of Research in Advent Technology 7 (2019) 268. https://doi.org/10.32622/ijrat.752019214.

P. V. Nirmaladevi, K.Lakshminarayanachari & C. Pandurangappa “ThreeDimensional Analytical Model for the Dispersion of Air Pollutants Emitted from Elevated Point Source with Mesoscale Wind and Removal Mechanism” J. Comput. Theor. Nanosci. 15,(2018), 3287–3290, https://doi.org/10.1166/jctn.2018.7612.

K. Ravindranath, K.Lakshminarayanachari & C. Pandurangappa “Time dependent analytical diffusion model of air pollutant in a protected zone due to point source with wet deposition”, J. Comput. Theor. Nanosci. 15 (2018) 3344. https://doi.org/10.1166/jctn.2018.7624.

Latha Rachachari, Lakshminarayanachari Kodandachari, Bhaskar Cholaraju, Two-dimensional analytical model for an air pollutants emitted from line source with mesoscale wind. AIP Conf. Proc. 2649 (2023) 030043. https://doi.org/10.1063/5.0117157.

L. Rachachari, L. Kodandachari & B. Cholaraju, “Three-dimensional analytical model for point source with removal mechanisms dry and wet deposition”, AIP Conf. Proc. 2649 (2023) 030032. https://doi.org/10.1063/5.0117156.

R. T. McNider, & A. Pour-Biazar, “Meteorological modeling relevant to mesoscale and regional air quality applications: a review”, Journal of the Air & Waste Management Association 7 (2019) 43. https://doi.org/10.1080/10962247.2019.1694602.

B. Chitturi, L. Lakshminarayanachari & C. Pandurangappa, “Analytical approach for air pollution emitted from an elevated point source with mesoscale wind”’, Journal of Computational and Theoretical Nanoscience 15 (2018) 3553. https://doi.org/10.1166/jctn.2018.7662

J. B. Johnson, “An Introduction to atmospheric pollutant dispersion modelling”, Environ. Sci. Proc. 19 (2022) 18. https://doi.org/10.3390/ecas2022-12826.

R. Kunchitiga & L. Kodandachari, “Mathematical time dependent diffusion model of air pollution with settling and wet deposition of larger particles of pollutants due to area sources in a protected zone”, AIP Conf. Proc. 2649 (2023) 030046. https://doi.org/10.1063/5.0146712.

J. Kafle, K. P. Adhikari, E. P. Poudel & R. R. Pant, “Mathematical modeling of pollutants dispersion in the atmosphere”, Journal of Nepal Mathematical Society 7 (2024) 61. https://doi.org/10.3126/jnms.v7i1.67487.

Published

2024-09-26

How to Cite

An analytical model for point source pollutants  in an urban area with mesoscale wind and wet deposition. (2024). Journal of the Nigerian Society of Physical Sciences, 6(4), 2116. https://doi.org/10.46481/jnsps.2024.2116

Issue

Volume 6, Issue 4, November 2024

Section

Mathematics & Statistics
Copyright & Licensing

Copyright (c) 2024 R. Latha, K. Lakshminarayanachari, C. Bhaskar

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

An analytical model for point source pollutants  in an urban area with mesoscale wind and wet deposition. (2024). Journal of the Nigerian Society of Physical Sciences, 6(4), 2116. https://doi.org/10.46481/jnsps.2024.2116