Understanding normal and restricted normal products in soft directed graphs
Keywords:
Soft Graph, Soft Directed Graph, Normal ProductAbstract
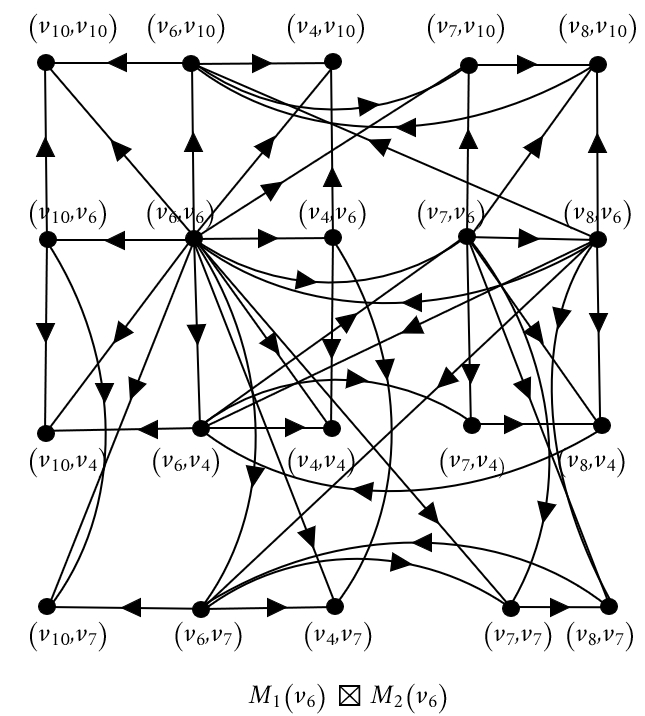
This paper extends the framework of soft set theory to directed graphs by introducing and analyzing the concepts of the normal product and restricted normal product of soft directed graphs. Building on Molodtsov’s foundational work in developing soft set theory to address uncertainty in data, this study presents new methods for modeling and understanding complex systems where uncertainty plays a significant role. Soft directed graphs, which enhance traditional graph models by incorporating parameters and uncertain relationships, serve as the foundation for this investigation. The normal product, defined as a combination of two soft directed graphs based on their respective parameter sets, and the restricted normal product, which combines soft directed graphs only where their parameter sets intersect, provide a comprehensive framework for these new operations. This paper also establishes the structural properties of these products, ensuring they are well-defined and retain the key features of soft directed graphs. Furthermore, we derive combinatorial identities related to vertex and arc counts, as well as degree sums, offering deeper insights into the composition and behavior of these graph products.
Published
How to Cite
Issue
Section
Copyright (c) 2024 Jinta Jose, Bobin George, Rajesh K. Thumbakara, Sijo P. George

This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
Most read articles by the same author(s)
- Jinta Jose, Rajesh K. Thumbakara, J. D. Thenge Mashale, Bobin George, Sijo P. George, Homomorphic and restricted homomorphic products of soft graphs , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 1, February 2025







