Homomorphic and restricted homomorphic products of softgraphs

Abstract

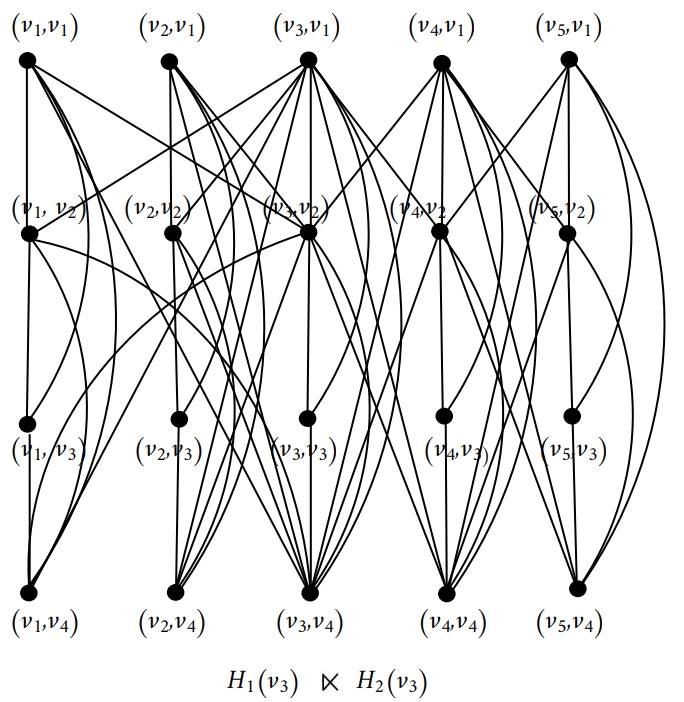
Molodtsov pioneered the notion of soft set theory, presenting it as a mathematical tool for dealing with uncertainty. Numerous researchers have subsequently developed models leveraging this theory to tackle challenges in decision-making and medical diagnosis. Soft set theory emerges as a flexible framework adept at handling uncertain and imprecise information, a domain where classical set theory often struggles. Expanding on the soft set concept, researchers have introduced the idea of a soft graph. This innovative concept allows for the creation of diverse representations of graph-based relations by incorporating parameterisation. In this work, we present and investigate some of the features of the homomorphic and restricted homomorphic products of soft graphs. This paper establishes the structural properties of these products, ensuring that they are well-defined and maintain the essential characteristics of soft graphs. Additionally, we derive combinatorial identities related to the counts of vertices and edges, as well as the degree sums, offering deeper insights into the composition and behaviour of these graph products.