Onchocerciasis control via Caputo-Fabrizio fractional dynamics: a focus on early treatment and vector management strategies

Authors

  • Danat Nanle Tanko
    School of Mathematical Sciences, Universiti Sains Malaysia, 11800 USM, Pulau Pinang, Malaysia
    Department of Mathematics, Plateau State University Bokkos, 2012 Jos, Plateau State, Nigeria
  • Farah Aini Abdullah
    School of Mathematical Sciences, Universiti Sains Malaysia, 11800 USM, Pulau Pinang, Malaysia
    https://orcid.org/0000-0002-5215-9617
  • Majid K. M Ali
    School of Mathematical Sciences, Universiti Sains Malaysia, 11800 USM, Pulau Pinang, Malaysia
  • Matthew O. Adewole
    School of Mathematical Sciences, Universiti Sains Malaysia, 11800 USM, Pulau Pinang, Malaysia.
    Department of Computer Science and Mathematics, Mountain Top University, Prayer City, Ogun State, Nigeria
  • James Andrawus
    Department of Mathematics, Federal University, Dutse 7156, Jigawa, Nigeria

Keywords:

Caputo-Fabrizio fractional derivative, Existence, Stability, Fractional Adams-Bashforth Numerical scheme, Onchocerciasis model

Abstract

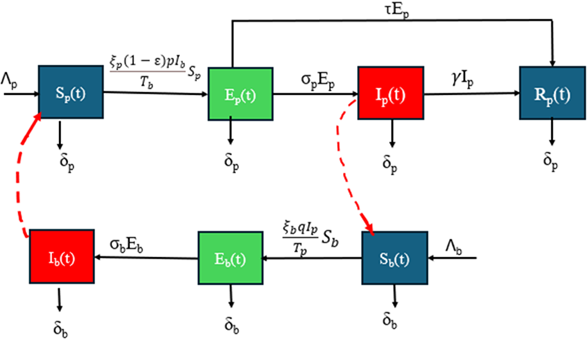
The socio-economic burdens of onchocerciasis have prompted the formulation of several mathematical models to better comprehend the epidemic. However, existing models either use integer-order derivatives, which often do not capture the memory and non-local effects seen in infectious diseases, or fractional order with singularity kernels, which may inadequately represent memory effects due to their singularity kernels. Onchocerciasis has a prolonged incubation and slow progression, making past conditions impactful on the disease's current and future course. Fractional derivatives effectively capture this memory effect, providing a more realistic depiction of the infection dynamics than integer-order models. We propose a non-local, non-singular exponential kernel fractional-order onchocerciasis model in the Caputo-Fabrizio fractional derivative sense to capture the disease's memory effects. Our model incorporates early treatment of exposed individuals as a critical intervention parameter, and vector management strategies are also incorporated. Using fixed-point theorem and iterative methods, we establish the existence and uniqueness of solutions, derive conditions for onchocerciasis-free and endemic equilibrium points, and analyze their stability, confirming the model's biological feasibility. Numerical simulations are conducted using a three-step fractional Adams-Bashforth method. Sensitivity analyses indicate that vector management and early treatment effectively reduce the effective reproduction number, while increases in the human-to-vector contact rate elevate it. Numerical results demonstrate that early treatment and vector management can significantly control onchocerciasis. The fractional-order "memory effect" highlights the importance of continuous monitoring and consistent application of control measures to reduce the memory index and curb onchocerciasis prevalence over time.

Dimensions

[1] H. C. Turner, M. Walker, M. D. French, I. M. Blake, T. S. Churcher & M. G. Basanez, “Neglected tools for neglected diseases: mathematical models in economic evaluations”, Trends in parasitology 30 (2014) 562. https://doi.org/10.1016/j.pt.2014.10.001.

[2] S. Jawahar, N. Tricoche, C. A. Bulman, J. Sakanari & S. Lustigman, “Drugs that target early stages of onchocerca volvulus: A revisited means to facilitate the elimination goals for onchocerciasis”, PLoS Neglected Tropical Diseases 15 (2021) 0009064. https://doi.org/10.1371/journal.pntd.0009064.

[3] P. T. Cantey, S. L. Roy, D. Boakye, U. Mwingira, E. A. Ottesen, A. D. Hopkins & Y. K. Sodahlon, “Transitioning from river blindness control to elimination: steps toward stopping treatment”, International health 10 (2018) 7. https://doi.org/10.1093/inthealth/ihx049.

[4] R. S. Nicholls, S. Duque, L. A. Olaya, M. C. Lopez, S. B. S ´ anchez, A. L. Morales & G. I. Palma, “Elimination of onchocerciasis from Colombia: first proof of concept of river blindness elimination in the world”, Parasites & vectors 11 (2018) 1. https://doi.org/10.1186/s13071-018-2821-9.

[5] M. Sauerbrey, L. J. Rakers & F. O. Richards, “Progress toward elimination of in the Americas”, International health 10 (2018) 71. https://doi.org/10.1093/inthealth/ihx039.

[6] D. N. Udall, “Recent updates on onchocerciasis: diagnosis and treatment”, Clinical infectious diseases 44 (2007) 53. https://doi.org/10.1086/509325.

[7] L. Frallonardo, F. Di Gennaro, G. G. Panico, R. Novara, E. Pallara, S. Cotugno, G. Guido, E. De Vita, A. Ricciardi, V. Totaro et al., “Onchocerciasis: current knowledge and future goals”, Frontiers in Tropical Diseases 3 (2022) 986884. https://doi.org/10.3389/fitd.2022.986884.

[8] R. K. Prichard, M.-G. Basanez, B. A. Boatin, J. S. McCarthy, H. H. Garcia, G. J. Yang, B. Sripa & S. Lustigman, “A research agenda for helminth diseases of humans: intervention for control and elimination”, PLoS neglected tropical diseases 6 (2012) 1549. https://doi.org/10.1371/journal.pntd.0001549.

[9] S. Lustigman, R. K. Prichard, A. Gazzinelli, W. N. Grant, B. A. Boatin, J. S. McCarthy & M.G. Basanez, “A research agenda for helminth diseases of humans: the problem of helminthiases”, PLoS neglected tropical diseases 6 (2012) 1582. https://doi.org/10.1371/journal.pntd.0001582.

[10] R. Tyagi, C. A. Bulman, F. Cho-Ngwa, C. Fischer, C. Marcellino, M. R. Arkin, J. H. McKerrow, C. W. McNamara, M. Mahoney, N. Tricoche et al., “An integrated approach to identify new antifilarial leads to treat river blindness, a neglected tropical disease”, Pathogens 10 (2021) 71. https://doi.org/10.3390/pathogens10010071.

[11] A. Plaisier, G. Van Oortmarssen, J. Remme & J. Habbema, “The reproductive lifespan of onchocerca volvulus in west african savanna”, Acta tropica 48 (1991) 271. https://doi.org/10.1016/0001-706X(91)90015-C.

[12] W. S. Alley, G. J. Van Oortmarssen, B. A. Boatin, N. J. Nagelkerke, A. P. Plaisier, J. H. Remme, J. Lazdins, G. J. Borsboom & J. D. F. Habbema, “Macrofilaricides and onchocerciasis control, mathematical modelling of the prospects for elimination”, BMC Public health 1 (2020) 12. https://doi.org/10.1186/1471-2458-1-12.

[13] P. Milton, J. I. Hamley, M. Walker & M.-G. Basa´nez, “Moxidectin: an oral treatment for human onchocerciasis”, Expert Review of AntiInfective Therapy 18 (2020) 1067. https://doi.org/10.1080/14787210.2020.1792772.

[14] N. Mutono, M.G. Basanez, A. James, W. A. Stolk, A. Makori, T. N. Kimani, T. D. Hollingsworth, A. Vasconcelos, M. A. Dixon, S. J. de Vlas et al., “Elimination of transmission of onchocerciasis (river blindness) with long-term ivermectin mass drug administration with or without vector control in sub-saharan Africa: a systematic review and metaanalysis”, The Lancet Global Health 12 (2024) 771. https://doi.org/10.1016/S2214-109X(24)00043-3.

[15] I. C. Oguoma and T. M. Acho, “Mathematical modelling of the spread and control of onchocerciasis in tropical countries: case study in Nigeria”, Abstract and Applied Analysis 2014 (2014) 631658. https://doi.org/10.1155/2014/631658.

[16] E. Omondi, F. Nyabadza & R. Smith, “Modelling the impact of mass administration of ivermectin in the treatment of onchocerciasis (river blindness)”, Cogent Mathematics & Statistics 5 (2018) 1429700. https://doi.org/10.1080/23311835.2018.1429700.

[17] K. Adeyemo, “Local stability analysis of onchocerciasis transmission dynamics with nonlinear incidence functions in two interacting populations”, European Journal of Mathematical Analysis 3 (2023) 22. https://doi.org/10.28924/ada/ma.3.22.

[18] M. Konlan, B. Abassawah Danquah, E. Okyere, S. Osman, J. Amenyo Kessie & E. Kobina Donkoh, “Global stability analysis and modelling onchocerciasis transmission dynamics with control measures”, Infection Ecology & Epidemiology 14 (2024) 11. https://doi.org/10.1080/20008686.2024.2347941.

[19] E. O. Omondi, F. Nyabadza, E. Bonyah & K. Badu, “Modeling the infection dynamics of onchocerciasis and its treatment”, Journal of Biological Systems 25 (2017) 247. https://doi.org/10.1142/S0218339017500139.

[20] E. O. Omondi, T. O. Orwa & F. Nyabadza, “Application of optimal control to the onchocerciasis transmission model with treatment”, Mathematical biosciences 297 (2018) 43. https://doi.org/10.1016/j.mbs.2017.11.009.

[21] M. G. Basa´nez, M. Walker, H. Turner, L. Co ˜ ffeng, S. De Vlas & W. Stolk, “River blindness: mathematical models for control and elimination”, Advances in parasitology 94 (2016) 247. https://doi.org/10.1016/bs.apar.2016.08.003.

[22] M. Walker, W. A. Stolk, M. A. Dixon, C. Bottomley, L. Diawara, M. O. Traore, S. J. De Vlas & M.G. Bas anez, “Modelling the elimination of river blindness using long-term epidemiological and programmatic data from mali and senegal”, Epidemics 18 (2017) 4. https://doi.org/10.1016/j.epidem.2017.02.005.

[23] I. Tirados, E. Thomsen, E. Worrall, L. Koala, T. T. Melachio & M.-G. Basa´nez, “Vector control and entomological capacity for onchocerciasis elimination”, Trends in parasitology 38 (2022) 591. https://doi.org/10.1016/j.pt.2022.03.003.

[24] M. Saeedian, M. Khalighi, N. Azimi-Tafreshi, G. Jafari & M. Ausloos, “Memory effects on epidemic evolution: The susceptible-infected recovered epidemic model”, Physical Review E 95 (2017) 022409. https://doi.org/10.1103/PhysRevE.95.022409.

[25] A. S. Shaikh, I. N. Shaikh & K. S. Nisar, “A mathematical model of covid19 using fractional derivative: outbreak in india with dynamics of transmission and control”, Advances in Difference Equations 2020 (2020) 373. https://link.springer.com/article/10.1186/s13662-020-02834-3.

[26] S. E. Fadugba, “Solution of fractional order equations in the domain of the mellin transform”, Journal of the Nigerian Society of Physical Sciences 5 (2023) 138. https://doi.org/10.46481/jnsps.2019.31.

[27] R. Agarwal, P. Airan & R. P. Agarwal, “Exploring the landscape of fractional-order models in epidemiology: A comparative simulation study.” Axioms 13 (2024) 13080545. https://doi.org/10.3390/axioms13080545.

[28] M. Vellappandi, P. Kumar & V. Govindaraj, “Role of fractional derivatives in the mathematical modeling of the transmission of chlamydia in the united states from 1989 to 2019”, Nonlinear Dynamics 111 (2023) 4915. https://doi.org/10.1007/s11071-022-08073-3.

[29] K. S. Nisar, M. Farman, M. Abdel-Aty & J. Cao, “A review on epidemic models in sight of fractional calculus”, Alexandria Engineering Journal 75 (2023) 81. https://doi.org/10.1016/j.aej.2023.05.071.

[30] P. Kumar, A. Kumar, S. Kumar & D. Baleanu, “A fractional order coinfection model between malaria and filariasis epidemic”, Arab Journal of Basic and Applied Sciences 31 (2024) 132. https://doi.org/10.1016/j.aej.2023.05.071.

[31] D. Baleanu, H. Mohammadi & S. Rezapour, “A fractional differential equation model for the covid-19 transmission by using the caputo–fabrizio derivative”, Advances in difference equations 2020 (2020) 299. https://doi.org/10.1016/j.aej.2023.05.071.

[32] J. Biazar, “Solution of the epidemic model by adomian decomposition method”, Applied Mathematics and Computation 173 (2006) 1101. https://doi.org/10.1016/j.amc.2005.04.036.

[33] K. Diethelm & N. J. Ford, “Analysis of fractional differential equations”, Journal of Mathematical Analysis and Applications 265 (2002) 229. https://doi.org/10.1006/jmaa.2000.7194.

[34] M. Ma, D. Baleanu, Y. S. Gasimov & X. J. Yang, “New results for multidimensional diffusion equations in fractal dimensional space”, Rom. J. Phys. 61 (2016) 784. https://doi.org/10.1006/jmaa.2000.7194.

[35] J. C. Blackwood & L. M. Childs, “An introduction to compartmental modeling for the budding infectious disease modeler”, Letters in Biomathematics 5 (2018) 195. https://doi.org/10.30707/LiB5.1Blackwood.

[36] A. O. Yunus & M. O. Olayiwola, “The analysis of a novel covid-19 model with the fractional-order incorporating the impact of the vaccination campaign in nigeria via the laplace-adomian decomposition method”, Journal of the Nigerian Society of Physical Sciences 6 (2024) 1830. https://doi.org/10.46481/jnsps.2024.1830.

[37] D. Baleanu, F. A. Ghassabzade, J. J. Nieto & A. Jajarmi, “On a new and generalized fractional model for a real cholera outbreak”, Alexandria Engineering Journal 61 (2022) 9175. https://doi.org/10.1016/j.aej.2022.02.054.

[38] A. I. K. Butt, “Atangana-baleanu fractional dynamics of predictive whooping cough model with optimal control analysis”, Symmetry 15 (2023) 1773. https://doi.org/10.3390/sym15091773.

[39] M. O. Adewole, T. S. Faniran, F. A. Abdullah & M. K. Ali, “Covid19 dynamics and immune response: Linking within-host and betweenhostdynamics”, Chaos, Solitons & Fractals 173 (2023) 113722. https://doi.org/10.1016/j.chaos.2023.113722.

[40] A. Atangana and R. T. Alqahtani, “Modelling the spread of river blindness disease via the caputo fractional derivative and the betaderivative”, Entropy 18 (2016) 40. https://doi.org/10.3390/e18020040.

[41] A. A. Onifade, P. O. Odeniran, I. O. Ademola, A. Yusuf & S. S. Musa, “Modeling the dynamics of onchocerca volvulus with the impact of environmental factors on blackfly breeding sites”, Scientific African 25 (2024) 02272. https://doi.org/10.1016/j.sciaf.2024.e02272.

[42] F. E. Guma, O. M. Badawy, M. Berir & M. A. Abdoon, “Numerical analysis of fractional-order dynamic dengue disease epidemic in sudan”, Journal of the Nigerian Society of Physical Sciences 5 (2023) 1464. https://doi.org/10.46481/jnsps.2023.1464.

[43] P. Kumar, S. Kumar, B. S. Alkahtani & S. S. Alzaid, “A mathematical model for simulating the spread of infectious disease using the caputofabrizio fractional-order operator”, AIMS Mathematics 9 (2024) 30864. https://doi.org/10.3934/math.20241490.

[44] M. Caputo and M. Fabrizio, “A new definition of fractional derivative without singular kernel”, Progress in Fractional Differentiation & Applications 1 (2024) 73. https://doi.org/10.12785/pfda/010201.

[45] D. Baleanu, A. Mousalou & S. Rezapour, “On the existence of solutions for some infinite coefficient-symmetric caputo-fabrizio fractional integrodifferential equations”, Boundary Value Problems 2017 (2017) 1. https://doi.org/10.1186/s13661-017-0867-9.

[46] D. K. Almutairi, M. A. Abdoon, S. Y. M. Salih, S. A. Elsamani, F. E. Guma & M. Berir, “Modeling and analysis of a fractional visceral leish-maniosis with caputo and caputo–fabrizio derivatives”, Journal of the Nigerian Society of Physical Sciences 5 (2023) 1453. https://doi.org/10.46481/jnsps.2023.1453.

[47] A. Shaikh, A. Tassaddiq, K. S. Nisar & D. Baleanu, “Analysis of differential equations involving caputo–fabrizio fractional operator and its applications to reaction–diffusion equations”, Advances in Difference Equations 2019 (2019) 1. https://doi.org/10.1186/s13662-019-2115-3.

[48] D. Baleanu, S. Rezapour & Z. Saberpour, “On fractional integrodifferential inclusions via the extended fractional caputo–fabrizio derivation”, Boundary Value Problems 2019 (2019) 1. https://doi.org/10.1186/s13661-019-1194-0.

[49] E. J. Moore, S. Sirisubtawee & S. Koonprasert, “A caputo– fabrizio fractional differential equation model for HIV/AIDS with treatment compartment”, Advances in Difference Equations 2019 (2019) 21389. https://doi.org/10.1186/s13662-019-2138-9.

[50] A. S. Alshehry, H. Yasmin, A. A. Khammash & R. Shah, “Numerical analysis of dengue transmission model using caputo–fabrizio fractional derivative”, Open Physics 22 (2024) 0169. https://doi.org/10.1515/phys-2023-0169.

[51] Y. M. Chu, M. F. Khan, S. Ullah, S. A. A. Shah, M. Farooq & M. bin Mamat, “Mathematical assessment of a fractional-order vector– host disease model with the caputo–fabrizio derivative”, Mathematical Methods in the Applied Sciences 22 (2024) 0169. https://doi.org/10.1002/mma.8507.

[52] K. M. Owolabi and A. Atangana, “Analysis and application of new fractional adams–bashforth scheme with caputo–fabrizio derivative”, Chaos, Solitons & Fractals 105 (2017) 111. https://doi.org/10.1016/j.chaos.2017.10.020.

[53] A. I. K. Butt, M. Imran, K. Azeem, T. Ismaeel & B. A. McKinney, “Analyzing hiv/aids dynamics with a novel caputofabrizio fractional order model and optimal control measures”, PloS one 19 (2019) 0315850. https://doi.org/10.1371/journal.pone.0315850.

[54] T. R. Nandi, A. K. Saha & S. Roy, “Analysis of a fractional order epidemiological model for tuberculosis transmission with vaccination and reinfection”, Scientific Reports 14 (2024) 28290. https://doi.org/10.1038/s41598-024-73392-x.

[55] J. Losada and J. J. Nieto, “Properties of a new fractional derivative without singular kernel”, Progr. Fract. Differ. Appl 1 (2015) 87. https://doi.org/10.12785/pfda/010202.

[56] T. Abdeljawad and D. Baleanu, “On fractional derivatives with exponential kernel and their discrete versions”, Reports on Mathematical Physics 80 (2017) 11. https://doi.org/10.1016/S0034-4877(17)30059-9.

[57] H. Yang, S. Qaisar, A. Munir & M. Naeem, “New inequalities via caputofabrizio integral operator with applications”, Aims Math 8 (2023) 19391. https://doi.org/10.3934/math.2023989.

[58] M. Khalighi, G. Sommeria-Klein, D. Gonze, K. Faust & L. Lahti, “Quantifying the impact of ecological memory on the dynamics of interacting communities”, PLoS computational biology 18 (2022) 1009396. https://doi.org/10.1371/journal.pcbi.1009396.

[59] H. F. Huo, R. Chen & X. Y. Wang, “Modelling and stability of hiv/aids epidemic model with treatment”, Applied Mathematical Modelling 40 (2016) 6550. https://doi.org/10.1016/j.apm.2016.01.054.

[60] P. Van den Driessche & J. Watmough, “Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission”, Mathematical biosciences 180 (2002) 29. https://doi.org/10.1016/S0025-5564(02)00108-6.

[61] M. Bani-Yaghoub, R. Gautam, Z. Shuai, P. Van Den Driessche & R. Ivanek, “Reproduction numbers for infections with freeliving pathogens growing in the environment”, Journal of biological dynamics 6 (2012) 923. https://doi.org/10.1080/17513758.2012.693206.

[62] H. Li, J. Cheng, H.-B. Li & S.-M. Zhong, “Stability analysis of a fractional-order linear system described by the caputo–fabrizio derivative”, Mathematics 7 (2019) 200. https://doi.org/10.3390/math7020200.

[63] U. T. Mustapha, Y. U. Ahmad, A. Yusuf, S. Qureshi & S. S. Musa, “Transmission dynamics of an age-structured hepatitis-b infection with differential infectivity”, Bulletin of Biomathematics 1 (2023) 124. https://doi.org/10.59292/bulletinbiomath.2023007.

[64] S. W. Teklu, “Mathematical analysis of the transmission dynamics of covid-19 infection in the presence of intervention strategies”, Journal of Biological Dynamics 16 (2022) 640. https://doi.org/10.1080/17513758.2022.2111469.

[65] S. Ajao, I. Olopade, T. Akinwumi, S. Adewale & A. Adesanya, “Understanding the transmission dynamics and control of hiv infection: A mathematical model approach”, Journal of the Nigerian Society of Physical Sciences 5 (2023) 1389. https://doi.org/10.46481/jnsps.2023.1389.

[66] Z. H. Shen, Y. M. Chu, M. A. Khan, S. Muhammad, O. A. Al-Hartomy, & M. Higazy, “Mathematical modeling and optimal control of the covid-19 dynamics”, Results in Physics 31 (2021) 105028. https://doi.org/10.1016/j.rinp.2021.105028.

[67] E. A. Nwaibeh and M. K. Ali, “Covid-19 dynamic modeling of immune variability and multistage vaccination strategies: a case study in malaysia”, Infectious Disease Modelling 10 (2025) 011. https://doi.org/10.1016/j.idm.2024.12.011.

[68] D. Gerbet & K. Robenack, “Application of Lasalle’s invariance principle “on polynomial differential equations using quantifier elimination”, IEEE Transactions on Automatic Control 67 (2025) 3590. https://doi.org/10.1109/TAC.2021.3103887.

[69] C. F. Lee, C. Y. Weng & C. Y. Kao, “Reversible data hiding using Lagrange interpolation for prediction-error expansion embedding”, Soft Computing 23 (2019) 9719. https://doi.org/10.1007/s00500-018-3537-7.

[70] Ghana Health Services, “Two-year strategic plan for integrated neglected tropical diseases control in ghana 2007–2008”, Ghana Health Services, 2016. http://www.moh-ghana.org/UploadFiles/Publications/Plan%20for%20Pro-Poor%20Diseases120506091943.pdf.

[71] D. Chicco, M. J. Warrens & G. Jurman, “The coefficient of determination R-squared is more informative than smape, mae, mape, mse and rmse in regression analysis evaluation”, Peerj computer science 7 (2021) 623. https://doi.org/10.7717/peerj-cs.623.

[72] A. D. W. Sumari, D. S. Charlinawati & Y. Ariyanto, “A simple approach using statistical-based machine learning to predict the weapon system operational readiness”, in Proceedings of the International Conference on Data Science and Official Statistics 2021 (2021) 343. https://doi.org/10.34123/icdsos.v2021i1.58

[73] Y. S. Lee and L. I. Tong, “Forecasting energy consumption using a grey model improved by incorporating genetic programming”, Energy conversion and Management 252 (2011) 147. https://doi.org/10.1016/j.enconman.2010.06.053.

[74] A. Hopkins and B. A. Boatin, “Onchocerciasis:water and sanitationrelated diseases and the environment: challenges, interventions, and preventive measures”, Scientific Reports 2011 (2011) 133. https://doi.org/10.1002/9781118148594.ch8.

[75] I. Onwubuya, G. Nkem, N. Tindi & C. Madubueze, “Optimal control analysis of onchocerciasis transmission model”, International Journal of Mathematical Analysis and Modelling 6 (2023) 1. https://tnsmb.org/journal/index.php/ijmam/article/view/78.

[76] J. C. Nguyen, M. M. E. Murphy, T. B. Nutman, R. C. Neafie, L. S. Maturo, D. S. Burke & C. G. W. Turiansky, “Cutaneous onchocerciasis in an american traveler”, International journal of dermatology 44 (2005) 125. https://doi.org/10.1111/j.1365-4632.2004.02203.x.

[77] A. Hassan and N. Shaban, “Onchocerciasis dynamics: modelling the effects of treatment, education and vector control”, Journal of Biological Dynamics 14 (2020) 245. https://doi.org/10.1080/17513758.2020.1745306.

[78] N. Chitnis, J. M. Hyman & J. M. Cushing, “Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model”, Bulletin of mathematical biology 14 (2020) 245. https://doi.org/10.1007/s11538-008-9299-0.

Published

2026-02-01

How to Cite

Onchocerciasis control via Caputo-Fabrizio fractional dynamics: a focus on early treatment and vector management strategies. (2026). Journal of the Nigerian Society of Physical Sciences, 8(1), 2942. https://doi.org/10.46481/jnsps.2026.2942

Issue

Volume 8, Issue 1, February 2026

Section

Mathematics & Statistics
Copyright & Licensing

Copyright (c) 2025 Danat Nanle Tanko, Farah Aini Abdullah, Majid K. M Ali, Matthew O. Adewole, James Andrawus (Author)

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Onchocerciasis control via Caputo-Fabrizio fractional dynamics: a focus on early treatment and vector management strategies. (2026). Journal of the Nigerian Society of Physical Sciences, 8(1), 2942. https://doi.org/10.46481/jnsps.2026.2942

Similar Articles

1-10 of 246

You may also start an advanced similarity search for this article.

Most read articles by the same author(s)