Analytical resolution of nonlinear fractional equations using the GERDFM method: Application to nonlinear Schrödinger and truncated Boussinesq-Burgers equations

Authors

  • Rachid El chaal
    Engineering Sciences Laboratory. Data Analysis, Mathematical Modeling, and Optimization Team, Department of Computer Science, Logistics and Mathematics, Ibn Tofail University National School of Applied Sciences ENSA, Kenitra 14000 Morocco
  • Hamid Dalhi
    Sidi Mohamed Ben Abdellah University, FSDM, Fez, Morocco
  • Otmane Darbal
    Sidi Mohamed Ben Abdellah University, FSDM, Fez, Morocco
  • Omar Boughaleb
    Sidi Mohamed Ben Abdellah University, FSDM, Fez, Morocco

Keywords:

Numerical modeling, GERDFM, Caputo derivative, Nonlinear Schrodinger equation, Fractional Runge-Kutta method 4

Abstract

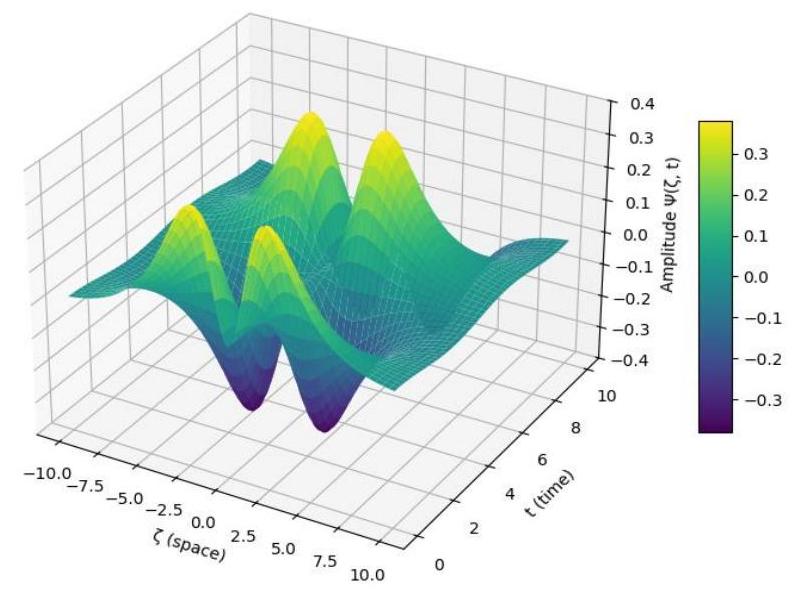
In this paper we develop the Generalized Exponential Rational Differential Function Method (GERDFM) for analytically solving complex nonlinear fractional partial differential equations, with application to the fractional nonlinear Schr¨odinger equation (NLSE) and the M-fractional truncated Boussinesq-Burgers equation. Our approach transforms these PDEs into adapted ordinary differential equations (ODEs), generating exact solutions for various nonlinear laws (Kerr, power, double power, parabolic) while explicitly incorporating the fractional Caputo derivatives of order M ? [0, 1]. The solitonic profiles obtained, illustrated by 2D/3D visualizations, reveal the crucial impact of non-linearity and fractional order on their dynamics, particularly in long memory optical systems and viscoelastic media. A rigorous numerical validation combining a fractional Runge-Kutta method and an L1 scheme confirms the superiority of our solutions, with a relative error < 10?8 (error < 2% near the solitonic peak) and a reduced computation time compared to conventional methods (Tanh-Coth, Sine-Cosine). These results open up concrete prospects for controlling solitons in anomalous dispersion optical fibers and modelling extreme waves in coastal hydrodynamics, while suggesting promising extensions to coupled and stochastic systems in nonlinear optics, fluid dynamics and plasma physics. This work provides significant advances in modeling wave propagation in complex media with memory effects. The GERDFM method’s ability to handle diverse nonlinearities while maintaining computational efficiency makes it particularly valuable for designing optical communication systems and predicting extreme wave phenomena in coastal engineering. Our analytical framework bridges a critical gap between classical soliton theory and fractional calculus applications.

Dimensions

[1] L. Ouahid, M. Alshahrani, A. M. Abdel-Baset, M. A. Abdou, A. Akgul¨ & M. K. Hassani, “Abundant soliton solutions in saturated ferromagnetic materials modeled via the fractional Kraenkel-MannaMerle system”, Sci Rep 15 (2025) 6763. https://doi.org/10.1038/s41598-024-78668-w. DOI: https://doi.org/10.1038/s41598-024-78668-w

[2] M. A. Bin Iqbal, M. Z. Raza, A. Khan, T. Abdeljawad & D. K. Almutairi, “Advanced wave dynamics in the STF-mBBM equation using fractional calculus”, Sci Rep 15 (2025) 5803. https://doi.org/10.1038/s41598-025-90044-w. DOI: https://doi.org/10.1038/s41598-025-90044-w

[3] B. I. Akinnukawe & K. O. Muka, “L-Stable block hybrid numerical algorithm for first-order ordinary differential equations”, J Niger Soc Phys Sci (2020) 160. https://doi.org/10.46481/jnsps.2020.108. DOI: https://doi.org/10.46481/jnsps.2020.108

[4] X. Duan & X. Wang, “On the orbital stability of Gross-Pitaevskii Solitons”, J Nonlinear Math Phys 32 (2025) 9. https://doi.org/10.1007/s44198-024-00257-2. DOI: https://doi.org/10.1007/s44198-024-00257-2

[5] M. Bilal, A. Khan, I. Ullah, H. Khan, J. Alzabut & H. M. Alkhawar, “ Application of modified extended direct algebraic method to nonlinear fractional diffusion reaction equation with cubic nonlinearity”, Bound Value Probl 2025 (2025) 16. https://doi.org/10.1186/s13661-025-01997-w. DOI: https://doi.org/10.1186/s13661-025-01997-w

[6] M. H. Bashar, M. A. Mannaf, M. M. Rahman & M. T. Khatun, “Optical soliton solutions of the M-fractional paraxial wave equation”, Sci Rep 15 (2025) 1416. https://doi.org/10.1038/s41598-024-74323-6. DOI: https://doi.org/10.1038/s41598-024-74323-6

[7] K. Bukht Mehdi et al., “Exploration of Soliton Dynamics and Chaos in the Landau-Ginzburg-Higgs Equation Through Extended Analytical Approaches”, J Nonlinear Math Phys 32 (2025) 22. https://doi.org/10.1007/s44198-025-00272-x. DOI: https://doi.org/10.1007/s44198-025-00272-x

[8] D. Iweobodo, G. Abanum, O. Ogoegbulem, N. Ochonogor & I. Njoseh, “Discretization of the Caputo time-fractional advection-diffusion problems with certain wavelet basis function”, J Niger Soc Phys Sci 7 (2025) 2405. https://doi.org/10.46481/jnsps.2025.2405. DOI: https://doi.org/10.46481/jnsps.2025.2405

[9] F. Wu, N. Raza, Y. Chahlaoui, A. R. Butt & H. M. Baskonus, “Phase Portraits and Abundant Soliton Solutions of a Hirota Equation with HigherOrder Dispersion”, Symmetry 16 (2024) 1554. https://doi.org/10.3390/sym16111554. DOI: https://doi.org/10.3390/sym16111554

[10] Y. Wang, G. Wang & Y. Zhang, “Exact solutions of a third-order nonlinear Schrodinger equation with time variable coe¨ fficients”, J Nonlinear Opt Phys Mater 34 (2025) 2450034. https://doi.org/10.1142/S0218863524500346. DOI: https://doi.org/10.1142/S0218863524500346

[11] B. I. Akinnukawe & S. A. Okunuga, “One-step block scheme with optimal hybrid points for numerical integration of second-order ordinary differential equations”, J Niger Soc Phys Sci 6 (2024) 1827. https://doi.org/10.46481/jnsps.2024.1827. DOI: https://doi.org/10.46481/jnsps.2024.1827

[12] M. A. S. Murad, H. F. Ismael & T. A. Sulaiman, “Resonant optical soliton solutions for time-fractional nonlinear Schrodinger equation in¨ optical fibers”, J Nonlinear Opt Phys Mater 34 (2025) 2450024. https://doi.org/10.1142/S0218863524500243. DOI: https://doi.org/10.1142/S0218863524500243

[13] M. Alosaimi, M. A. S. Al-Malki & K. A. Gepreel, “Optical soliton solutions in optical metamaterials with full nonlinearity”, J Nonlinear Opt Phys Mater 34 (2025) 2450021. https://doi.org/10.1142/S0218863524500218. DOI: https://doi.org/10.1142/S0218863524500218

[14] F. Obarhua & O. J. Adegboro, “An Order Four Continuous Numerical Method for Solving General Second Order Ordinary Differential Equations”, J Niger Soc Phys Sci 3 (2021) 42. https://doi.org/10.46481/jnsps.2021.150. DOI: https://doi.org/10.46481/jnsps.2021.150

[15] V. Kumar, A. Patel & M. Kumar, “Dynamics of solitons and modulation instability in a (2 + 1)−dimensional coupled nonlinear Schrodinger¨ equation”, Math Comput Simul 235 (2025) 95. https://doi.org/10.1016/j.matcom.2025.03.022. DOI: https://doi.org/10.1016/j.matcom.2025.03.022

[16] F. Guo & W. Dai, “A linear and mass conservative scheme for the thermal soliton model based on nonlinear Schrodinger and heat transfer equa-¨ tions”, J Comput Appl Math 464 (2025) 116529. https://doi.org/10.1016/j.cam.2025.116529. DOI: https://doi.org/10.1016/j.cam.2025.116529

[17] M. Vellappandi & S. Lee, “Physics-informed neural fractional differential equations”, Appl Math Model 145 (2025) 116127. https://doi.org/10.1016/j.apm.2025.116127. DOI: https://doi.org/10.1016/j.apm.2025.116127

[18] Q. Xin, X.-M. Gu & L.-B. Liu, “A fast implicit difference scheme with nonuniform discretized grids for the time-fractional Black-Scholes model”, Appl Math Comput 500 (2025) 129441. https://doi.org/10.1016/j.amc.2025.129441. DOI: https://doi.org/10.1016/j.amc.2025.129441

[19] J. Yu & Y. Feng, “Lie symmetries, exact solutions and conservation laws of time fractional Boussinesq-Burgers system in ocean waves”, Commun Theor Phys 76 (2024) 125002. https://doi.org/10.1088/1572-9494/ad71ab. DOI: https://doi.org/10.1088/1572-9494/ad71ab

[20] M.-D. Junjua, S. Altaf, A. A. Alderremy & E. E. Mahmoud, “Exact wave solutions of truncated M-fractional Boussinesq-Burgers system via an effective method”, Phys Scr 99 (2024) 095263. https://doi.org/10.1088/1402-4896/ad6ec9. DOI: https://doi.org/10.1088/1402-4896/ad6ec9

[21] S.-J. Li, S. Chai & I. Lasiecka, “Stabilization of a weak viscoelastic wave equation in Riemannian geometric setting with an interior delay under nonlinear boundary dissipation”, Nonlinear Anal Real World Appl 84 (2025) 104252. https://doi.org/10.1016/j.nonrwa.2024.104252. DOI: https://doi.org/10.1016/j.nonrwa.2024.104252

[22] I. Iqbal, F. M. Alsammak, M. Alsaeedi, M. E. E. Dalam & B. Iqbal, “Study of multi-term fractional delay differential equations involving Caputo-fractional derivative”, J Math Anal Appl 549 (2025) 129563. https://doi.org/10.1016/j.jmaa.2025.129563. DOI: https://doi.org/10.1016/j.jmaa.2025.129563

[23] M. M. Al-Sawalha, S. Mukhtar, A. S. Alshehry, M. Alqudah & M. S. Aldhabani, “Chaotic perturbations of solitons in complex conformable Maccari system”, AIMS Math 10 (2025) 6664. https://doi.org/10.3934/math.2025305. DOI: https://doi.org/10.3934/math.2025305

[24] L. Ouahid, “Abundant soliton solutions on fractional Kraenkel Manna Merle model (FKMM) via new extended of generalized exponential rational function approach (GERFA)”, Phys Scr 99 (2024) 065243. https://doi.org/10.1088/1402-4896/ad482a. DOI: https://doi.org/10.1088/1402-4896/ad482a

[25] Y. Wang, M. N. Raihen, E. Ilhan & H. M. Baskonus, “On the new sine-Gordon solitons of the generalized Korteweg-de Vries and modified Korteweg-de Vries models via beta operator”, AIMS Math 10 (2025) 5456. https://doi.org/10.3934/math.2025252. DOI: https://doi.org/10.3934/math.2025252

[26] M. Shahzad, R. Anjum, N. Ahmed, M. Z. Baber & N. Shahid, “On the closed form exact solitary wave solutions for the time-fractional order nonlinear unsteady convection diffusion system with unique-existence analysis”, Int J Geom Methods Mod Phys (2025) 2550128. https://doi.org/10.1142/S0219887825501282. DOI: https://doi.org/10.1142/S0219887825501282

[27] J. Muhammad et al., “Solitary wave solutions and sensitivity analysis to the space-time β-fractional Pochhammer-Chree equation in elastic medium”, Sci Rep 14 (2024) 28383. https://doi.org/10.1038/s41598-024-79102-x. DOI: https://doi.org/10.1038/s41598-024-79102-x

[28] N. Raza, A. Jhangeer, Z. Amjad, B. Rani & T. Muhammad, “Analyzing coupled-wave dynamics: lump, breather, two-wave and three-wave interactions in a (3 + 1)−dimensional generalized KdV equation”, Nonlinear Dyn 112 (2024) 22323. https://doi.org/10.1007/s11071-024-10199-5. DOI: https://doi.org/10.1007/s11071-024-10199-5

[29] B. Kopc¸asız, “Qualitative analysis and optical soliton solutions galore: scrutinizing the (2 + 1)−dimensional complex modified Korteweg-de Vries system”, Nonlinear Dyn 112 (2024) 21321. https://doi.org/10.1007/s11071-024-10036-9. DOI: https://doi.org/10.1007/s11071-024-10036-9

[30] Y. Saglam˘ Ozkan, “New exact solutions of the conformable spacetime¨ two-mode foam drainage equation by two effective methods”, Nonlinear Dyn 112 (2024) 19353. https://doi.org/10.1007/s11071-024-10010-5. DOI: https://doi.org/10.1007/s11071-024-10010-5

[31] H. Yoshioka, “Generalized Logit Dynamics Based on Rational Logit Functions”, Dyn Games Appl 14 (2024) 1333. https://doi.org/10.1007/s13235-023-00551-6. DOI: https://doi.org/10.1007/s13235-023-00551-6

[32] S. Yadav, A. K. Sharma & R. Arora, “Dynamical behaviours with various analytic solutions to a (2 + 1) extended Boiti-Leon-MannaPempinelli equation”, Pramana 98 (2024) 116. https://doi.org/10.1007/s12043-024-02784-5. DOI: https://doi.org/10.1007/s12043-024-02784-5

[33] J. Muhammad, U. Younas, N. Nasreen, A. Khan & T. Abdeljawad, “Multicomponent nonlinear fractional Schrodinger equation: On the study¨ of optical wave propagation in the fiber optics”, Partial Differ Equations Appl. Math 11 (2024) 100805. https://doi.org/10.1016/j.padiff.2024.100805. DOI: https://doi.org/10.1016/j.padiff.2024.100805

[34] S. U. Rehman, J. Ahmad, K. S. Nisar & A.-H. Abdel-Aty, “Stability analysis, lump and exact solutions to Sharma-Tasso-Olver-Burgers equation”, Opt Quantum Electron 56 (2024) 1227. https://doi.org/10.1007/s11082-024-06733-9. DOI: https://doi.org/10.1007/s11082-024-06733-9

[35] A. Mahmood et al., “Exact solutions of cubic-quintic-septimal nonlinear Schrodinger wave equation”, Opt Quantum Electron¨ 56 (2024) 1096. https://doi.org/10.1007/s11082-024-06907-5. DOI: https://doi.org/10.1007/s11082-024-06907-5

[36] A. E. Hamza, M. Suhail, A. Alsulami, A. Mustafa, K. Aldwoah & H. Saber, “Exploring Soliton Solutions and Chaotic Dynamics in the (3+1)−Dimensional Wazwaz-Benjamin-Bona-Mahony Equation: A Generalized Rational Exponential Function Approach”, Fractal Fract 8 (2024) 592. https://doi.org/10.3390/fractalfract8100592. DOI: https://doi.org/10.3390/fractalfract8100592

[37] U. Younas, J. Muhammad, N. Nasreen, A. Khan & T. Abdeljawad, “On the comparative analysis for the fractional solitary wave profiles to the recently developed nonlinear system”, Ain Shams Eng J 15 (2024) 102971. https://doi.org/10.1016/j.asej.2024.102971. DOI: https://doi.org/10.1016/j.asej.2024.102971

[38] U. Demirbilek, M. Nadeem, F. M. C¸elik, H. Bulut & M. S¸enol, “Generalized extended (2 + 1)−dimensional Kadomtsev-Petviashvili equation in fluid dynamics: analytical solutions, sensitivity and stability analysis”, Nonlinear Dyn 112 (2024) 13393. https://doi.org/10.1007/s11071-024-09724-3. DOI: https://doi.org/10.1007/s11071-024-09724-3

[39] B. Kopc¸asız & E. Yas¸ar, “M-truncated fractional form of the perturbed Chen-Lee-Liu equation: optical solitons, bifurcation, sensitivity analysis, and chaotic behaviors”, Opt Quantum Electron 56 (2024) 1202. https://doi.org/10.1007/s11082-024-07148-2. DOI: https://doi.org/10.1007/s11082-024-07148-2

[40] S. Ghosh, “A study on the fractional Black–Scholes option pricing model of the financial market via the Yang-Abdel-Aty-Cattani operator”, Engineering Computations 41 (2024) 611. https://doi.org/10.1108/EC-08-2023-0452. DOI: https://doi.org/10.1108/EC-08-2023-0452

[41] S. Ghosh, “An analytical approach for the fractional-order Hepatitis B model using new operator”, Int J Biom math 17 (2024) 2350008. https://doi.org/10.1142/S1793524523500080. DOI: https://doi.org/10.1142/S1793524523500080

[42] S. Ghosh, “Numerical Study on Fractional-Order Lotka-Volterra Model with Spectral Method and Adams–Bashforth–Moulton Method”, Int J Appl Comput Math 8 (2022) 34. https://doi.org/10.1007/s40819-022-01457-4. DOI: https://doi.org/10.1007/s40819-022-01457-4

[43] J. Sylvia, S. Ghosh, “Numerical study of a chemical clock reaction framework utilizing the Haar wavelet approach”, J Math Chem 63 (2025) 1241. https://doi.org/10.1007/s10910-025-01719-8. DOI: https://doi.org/10.1007/s10910-025-01719-8

[44] J. Sylvia, S. Ghosh, “Solution of chemical reaction model using Haar wavelet method with Caputo derivative”, J Math Chem 62 (2024) 2222. https://doi.org/10.1007/s10910-024-01654-0. DOI: https://doi.org/10.1007/s10910-024-01654-0

Published

2025-08-18

How to Cite

Analytical resolution of nonlinear fractional equations using the GERDFM method: Application to nonlinear Schrödinger and truncated Boussinesq-Burgers equations. (2025). Journal of the Nigerian Society of Physical Sciences, 7(4), 2953. https://doi.org/10.46481/jnsps.2025.2953

Issue

Volume 7, Issue 4, November 2025 (In Progress)

Section

Mathematics & Statistics
Copyright & Licensing

Copyright (c) 2025 Rachid El chaal, Hamid Dalhi, Otmane Darbal, Omar Boughaleb (Author)

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Analytical resolution of nonlinear fractional equations using the GERDFM method: Application to nonlinear Schrödinger and truncated Boussinesq-Burgers equations. (2025). Journal of the Nigerian Society of Physical Sciences, 7(4), 2953. https://doi.org/10.46481/jnsps.2025.2953

Most read articles by the same author(s)