An Epidemic Model of Zoonotic Visceral Leishmaniasis with Time Delay
Keywords:
ZVL, Stability, Hopf bifurcation, Time delayAbstract
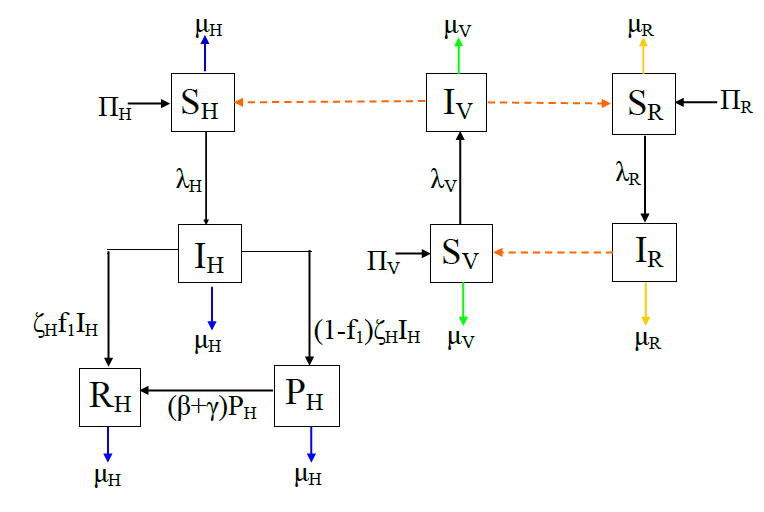
This paper presents a mathematical model with time delay for the transmission dynamics of zoonotic visceral leishmaniasis (ZVL which is caused by protozoan parasite leishmania infantum and transmitted by female sandflies). Qualitative analysis of the ODE version of the model reveals that the disease-free equilibrium of the model is globally asymptotically stable when the basic reproduction number, R0, is less than unity. Using time delay as a bifurcation parameter in the delay-differential version of the model, it has been shown that the incubation period has a significant effect on the stability of the equilibria and we derived the condition for Hopf bifurcation to occur.
Published
How to Cite
Issue
Section
Copyright (c) 2019 Journal of the Nigerian Society of Physical Sciences

This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
Similar Articles
- V. J. Shaalini, S. E. Fadugba, A New Multi-Step Method for Solving Delay Differential Equations using Lagrange Interpolation , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 3, August 2021
- Saheed Ajao, Isaac Olopade, Titilayo Akinwumi, Sunday Adewale, Adelani Adesanya, Understanding the Transmission Dynamics and Control of HIV Infection: A Mathematical Model Approach , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 2, May 2023
- Helen Olaronke Edogbanya, Emmanuel Sabastine, Rosalio G. Artes Jr., Regimar A. Rasid, Dynamical and optimal control analysis of lymphatic filariasis and buruli ulcer co-infection , Journal of the Nigerian Society of Physical Sciences: Volume 6, Issue 4, November 2024
- Elsammani Ali Shokralla, Improving the thermal stability and dielectric properties of epoxy/phenolic resin type (novolac) composites by incorporating carbon nanofibers (CNFs) , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 1, February 2025
- Anthony Anya Okeke, Nur Nadiah Abd Hamid, Wen Eng Ong, Muhammad Abbas, A numerical algorithm based on extended cubic B-spline functions for solving time-fractional convection-diffusion-reaction equation with variable coefficients , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 1, February 2025
- Adamu Shitu Hassan, Nafiu Hussaini, Analysis of an HIV - HCV simultaneous infection model with time delay , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 1, February 2021
- Mahesh Kumar Singh, Pushpa Choudhary, Arun Kumar Singh, Pushpendra Singh, LWRNPIP: Design of a light weight restrictive non-fungible token based on practically unclonable functions via image signature patterns , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 4, November 2025
- Fathelrhman EL Guma, Ossama M. Badawy, Mohammed Berir, Mohamed A. Abdoon, Numerical Analysis of Fractional-Order Dynamic Dengue Disease Epidemic in Sudan , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 2, May 2023
- Mark I. Modebei, Olumide O. Olaiya, Ignatius P. Ngwongwo, Computational study of a 3-step hybrid integrators for third order ordinary differential equations with shift of three off-step points , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 4, November 2021
- S. A. Abdullahi, A. G. Habib, N. Hussaini, Mathematical Model of In-host Dynamics of Snakebite Envenoming , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 2, May 2022
You may also start an advanced similarity search for this article.
Most read articles by the same author(s)
- S. A. Abdullahi, A. G. Habib, N. Hussaini, Mathematical Model of In-host Dynamics of Snakebite Envenoming , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 2, May 2022






