Enhanced methods for multicollinearity mitigation in stochastic frontier analysis estimation
Keywords:
Stochastic Frontier Analysis, Multicollinearity, Assumption Violations, Correction MethodologiesAbstract
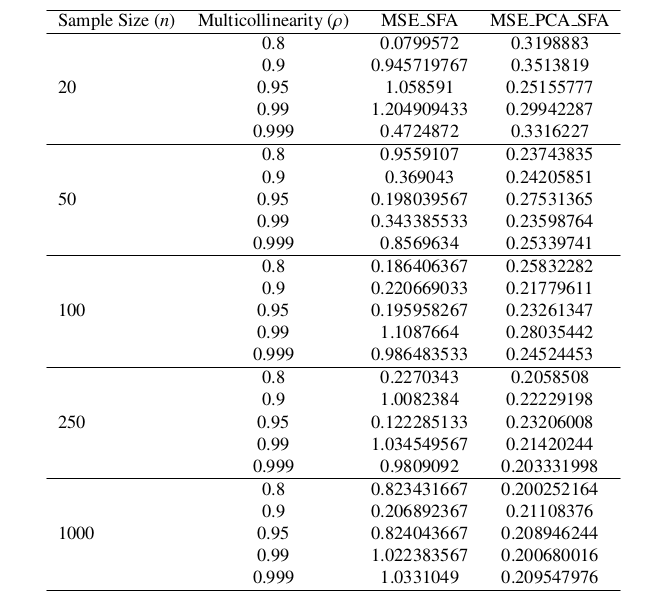
Efficiency estimation in production technology has been a concern in economics, with methodologies such as Stochastic Frontier Analysis (SFA) playing a key role in this area. SFA has been pivotal in evaluating the efficiency of entities by isolating technical inefficiency from random production errors. However, despite its significance, the application of SFA faces challenges when the multicollinearity assumption underlying the model is violated. Therefore, this study presents a novel estimator, termed “Principal Component Analysis Estimation for Stochastic Frontier Analysis” (PCA-SFA), to address the problem of multicollinearity in the classical SFA model. The PCA-SFA estimator integrates Principal Component Analysis (PCA) to correct assumption violation arising from multicollinearity. Monte Carlo simulation study was conducted to ascertain the PCA-SFA performance, involving no fewer than 2,000 replications based on the Cobb-Douglas production function with varying levels of multicollinearity, represented by correlation coefficients ranging from 0.8, 0.9, 0.95, 0.99, and 0.999, and sample sizes (n) of 20, 50, 100, 250, and 1,000. The proposed estimator’s performance was compared to the classical SFA model using the Mean Square Error (MSE), Akaike Information Criterion (AIC), and Bayesian Information Criterion (BIC) as evaluation metrics. The results demonstrate that the PCA-SFA estimator consistently outperforms the classical SFA model. The PCA-SFA model showed significantly lower MSE, AIC, and BIC values, indicating improved precision and reliability in parameter estimation. The study, therefore, recommends that researchers and practitioners in econometrics and related fields consider integrating PCA-SFA into their production efficiency analytical frameworks, particularly when dealing with datasets prone to multicollinearity issues.
Published
How to Cite
Issue
Section
Copyright (c) 2024 Rauf I. Rauf, Ayinde Kayode, Bello A. Hamidu, Bodunwa O. Kikelomo, Alabi O. Olusegun

This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
Most read articles by the same author(s)
- Abiola T. Owolabi, Kayode Ayinde, Taiwo J. Adejumo, Wakeel A. Kasali, Emmanuel T. Adewuyi, Comparative Analysis of the Implication of Periods Before and During Vaccination of COVID-19 Infection in Some Regional Leading African Countries , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 2, May 2022
- Segun L. Jegede, Adewale F. Lukman, Kayode Ayinde, Kehinde A. Odeniyi, Jackknife Kibria-Lukman M-Estimator: Simulation and Application , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 2, May 2022






