Effect of radial non-uniformity on mechanical response of functionally graded discs

Abstract

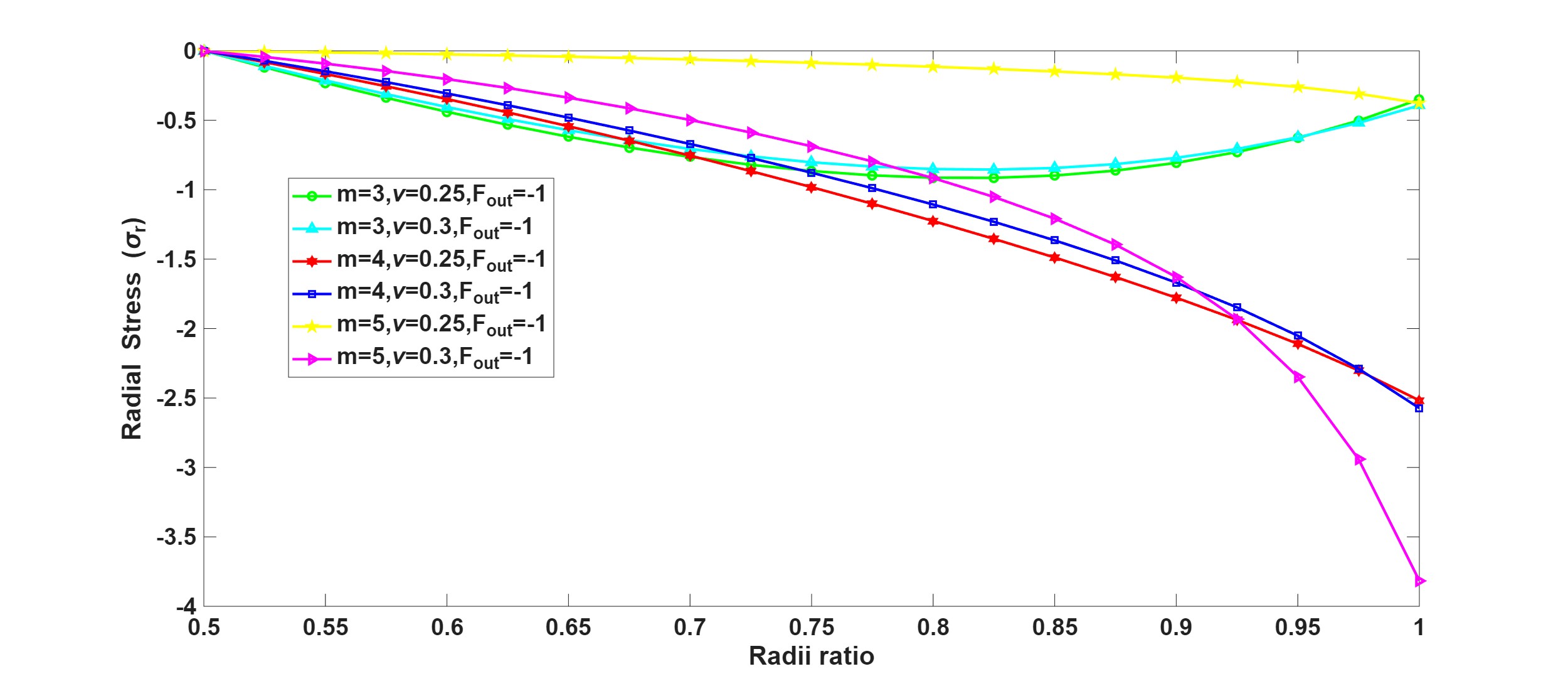
This study investigates the stress distribution in functionally graded material (FGM) discs composed of compressible and incompressible constituents, subjected to nonhomogeneity and external loading. Analytical results are presented for radial and tangential stresses as functions of the radii ratio r/b the gradation parameter m, and Poisson’s ratio $\nu$. However, the combined effect of compressibility and material gradation on the stress response of discs remains insufficiently explored, particularly in cases where both compressible (\nu < 0.5) and incompressible (\nu \rightarrow 0.5) material behaviors are considered under identical loading conditions. The methodology is designed to systematically evaluate how radial stress (\sigma_r) and tangential stress (\sigma_\theta) evolve across the disc geometry in response to the combined influences of material gradation and volumetric compressibility. Figures are generated by MATLAB to provide comparative insights, separating compressible and incompressible cases, and highlighting the stress sensitivity to parameter variations. The focus of the investigation is twofold. First, the study seeks to establish the relationship between Poisson’s ratio and stress magnitudes, particularly assessing whether compressible materials exhibit sharper stress gradients that could lead to structural instability. Second, the work examines the extent to which nonhomogeneity, represented by the parameter m, modifies these trends in both compressible and incompressible regimes. Furthermore, by delineating the contrasting behavior of compressible and incompressible FGMs, the study provides a decision-making basis for selecting appropriate material gradations in scenarios where crack initiation, fatigue resistance, or tensile failure are of concern. Thus, the present work sets out to systematically examine how compressibility and gradation interact to determine stress responses in FGM discs, with the ultimate objective of offering practical guidelines for the safe and efficient application of these advanced materials in engineering design.