A Purusit Differential Game Problem on a Closed Convex Subset of a Hilbert Space

Authors

  • Abbas Ja'afaru Badakaya
    Department of Mathematical Sciences, Bayero University, Kano
  • Bilyaminu Muhammad
    Department of Mathematics,Federal College of Eduction(Technical), Gusau, Zamfara State

Keywords:

Pursuit, integral constraint, closed convex set.

Abstract

We study a pursuit differential game problem with finite number of pursuers and one evader on a nonempty closed convex subset of the Hilbert space l2. Players move according to certain first order ordinary differential equations and control functions of the pursuers and evader are subject to integral constraints. Pursuers win the game if the geometric positions of a pursuer and the evader coincide. We formulated and prove theorems that are concern with conditions that ensure win for the pursuers. Consequently, wining strategies of the pursuers are constructed. Furthermore, illustrative example is given to demonstrate the result.

Dimensions

I. D. Alias , G. I. Ibragimov , M. Ferrra, M. Salimi, & M. Monsi , “Differential Game of Many Pursuers with Integral Constraints on a Convex set in the plane” (2015) arXiv:1505.00054v1[math.OC].

A. J. Badakaya, “Value of a Di erential Game Problem with Multiple Players in a Certain Hilbert Space”, Journal of the Nigerian Mathematical Society 36 (2017) 287.

H. H. Bauschke & P. L . Combettes Convex Analysis and Monotone Operator Theory in Hilbert Spaces Springer (2011).

C. E. Chidume, Applicable Functional Analysis, Ibadan University Press, (2014).

T. Gerald, Functional Analysis, Wien Australia, (2007).

G. Ibragimov & N. A. Hussin, “A Pursuit-Evasion Di erential Game with Many Pursuers and One Evader”, Malaysian Journal of Mathematical Sciences 4 (2010) 183.

G. I. Ibragimov, & B. B. Rikhsiev, “On some Sufficient Conditions for Optimalty of the Pursuit Time in the Differential Game with Multiple Pusuers”, Automation and Remote Control, 67 (2006) 529.

G. I. Ibragimov, A Game Problem on a Closed Convex Set”, Siberian Advances in Mathematics 12 (2002) 1 .

G. I. Ibragimov, & M. Salimi, “Pursuit-Evasion Differential Game with Many Inertial Players”, Mathematical Problems in Engineering, (2009)doi:10.1155/2009/653723.

G. Ibragimov, & N. Satimov, “A Multiplayer Pursuit Di erential Game on a Convext Set with Integral Constraints”, Abstract and Applied Analysis (2012)doi: 10.1155/2012/460171,.

G. I. Ibragimov, “Collective Pursuit with Integral Constraints on the Control of Players”, Siberian Advances in Mathematics 42 (2004) 1.

G. I. Ibragimov, “Optimal pursuit with countably many pursuers and one evader”, Differential Equations 41 (5) (2005) 627.

G. I. Ibragimov, “A Game of Optimal Pursuit of One Object by Several”, Journal of Applied Mathematics and Mechanics 62 (1998) 187.

G. Ibragimov, N. Abd Rashid, A. Kuchkarov, & F. Ismail, “Multi Pursuer Differential Game of Optimal Approach with Integral Constraints on Controls of the Players” , Taiwanese Journal of Mathematics 19 (2015)

R. P. Ivanov, & Yu. S. Ledyaev, “Optimality of pursuit time in a simple motion differential game of many objects”, Trudy Matematicheskogo Instituta imeni V. A. Steklova 158 (1981) 87.

A. B. Ja’afaru, & G. I. Ibragimov, ”On Some Pursuit and Evasion Differential Game Problems for an Infinite Numberof First-Order Differential Equations”, Journal of Applied Mathematics, 12 (2012) 13. doi:10.1155/2012/717124.

R. Juwaid, & A. J. Badakaya, “Pursuit Di erential Game Problem with Integral and Geometric Constraints in a Hilbert Space”, Journal of the Nigerian Mathematical Society 37 (2018) 203.

W. J. Leong, & I. G. Ibragimov, “A Multiperson Pursuit Problem on a Closed Convex Set in Hilbert Space”, Far East Journal of Applied Mathematics 33 (2008) 205.

A. Yu. Levchenkov, & A. G. Pashkov, “Differential Game of Optimal Approach of Two Inertial Pursuers to a Noninertial Evader”, Journal of Optimization Theory and Applications 65 (1990) 501 .

J. Yeh, “Real Analysis Theory of Measure and Integration”, World Scientific Publishing,(2006).

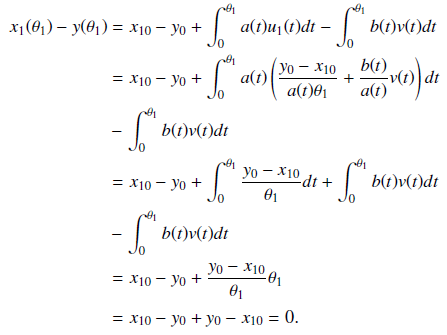
Published

2020-08-01

How to Cite

A Purusit Differential Game Problem on a Closed Convex Subset of a Hilbert Space. (2020). Journal of the Nigerian Society of Physical Sciences, 2(3), 115-119. https://doi.org/10.46481/jnsps.2020.82

Issue

Volume 2, Issue 3, August 2020

Section

Original Research
Copyright & Licensing

How to Cite

A Purusit Differential Game Problem on a Closed Convex Subset of a Hilbert Space. (2020). Journal of the Nigerian Society of Physical Sciences, 2(3), 115-119. https://doi.org/10.46481/jnsps.2020.82

Similar Articles

51-60 of 60

You may also start an advanced similarity search for this article.