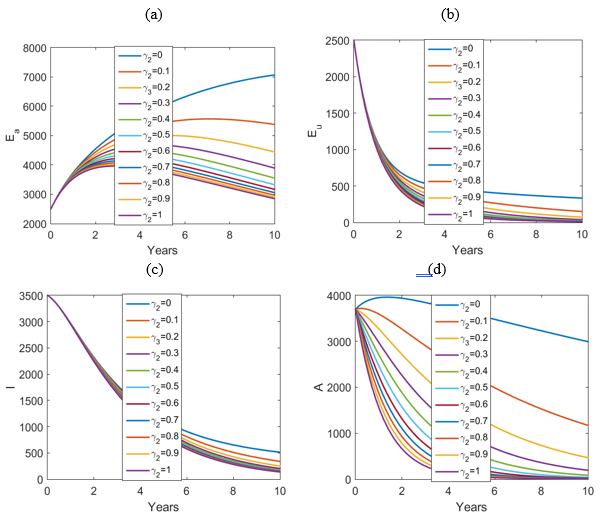
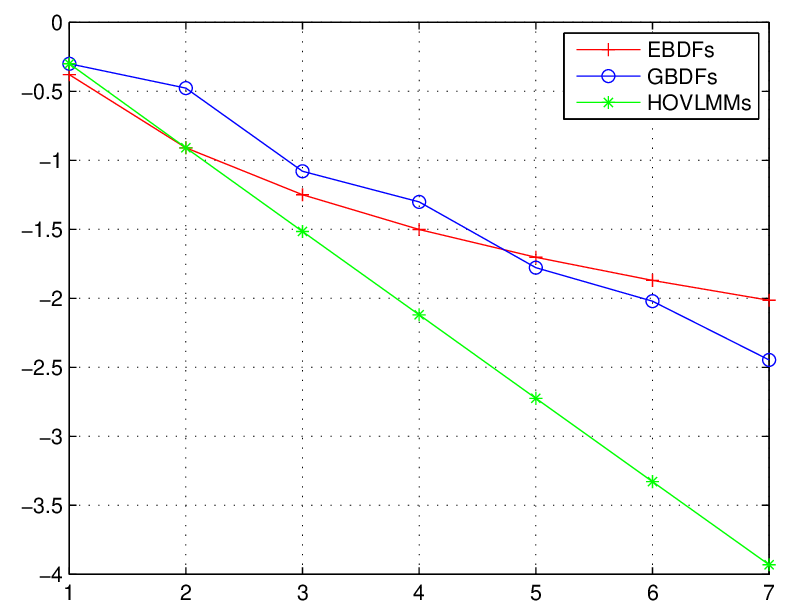
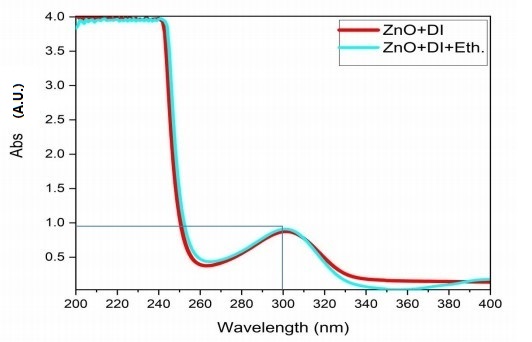
Important Update on Article Processing Charges (APC)
This is to notify the academic community that, effective June 1, 2025, Nigerian authors who are not registered members of the Nigerian Society of Physical Sciences (NSPS) will no longer be eligible for discounted Article Processing Charges (APC) in the Journal of the Nigerian Society of Physical Sciences (JNSPS). Consequently, non-member Nigerian authors will be required to pay the Naira equivalence of the full APC rate applicable to international authors.
Read more about Important Update on Article Processing Charges (APC)