Integrating robust feature selection with deep learning for ultra-high-dimensional survival analysis in renal cell carcinoma

Shaymaa Mohammed Ahmed; Majid Khan Majahar Ali; Raja Aqib Shamim

doi:10.46481/jnsps.2025.2772

Authors

Shaymaa Mohammed Ahmed School of Mathematical Sciences, Universiti Sains Malaysia, 11800, Pulau Penang, Malaysia https://orcid.org/0009-0008-6653-399X
Majid Khan Majahar Ali
[email protected]
School of Mathematical Sciences, Universiti Sains Malaysia, 11800, Pulau Penang, Malaysia https://orcid.org/0000-0002-5558-5929
Raja Aqib Shamim School of Mathematical Sciences, Universiti Sains Malaysia, 11800, Pulau Penang, Malaysia https://orcid.org/0000-0002-2531-1249

Keywords:

Ultra-High-Dimensional Survival Analysis, Renal Cell Carcinoma (RCC), Feature Selection with Deep Learning, Robust SIS, Robust ISIS

Abstract

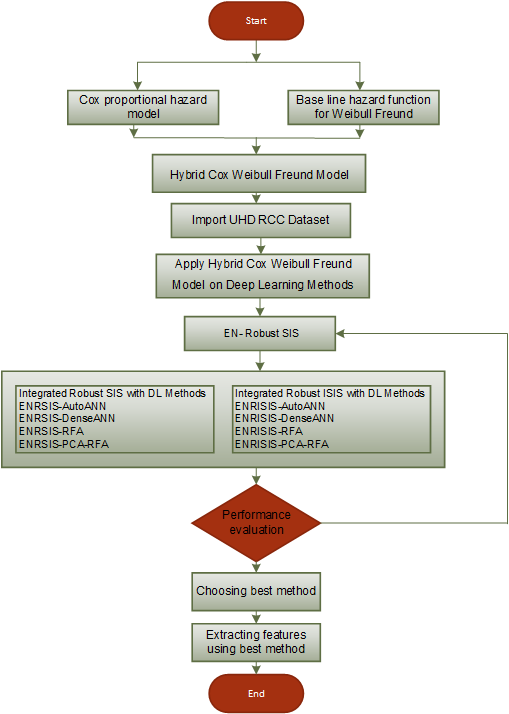
The research method applies robust feature selection approaches to ultra-high-dimensional survival data records from Renal Cell Carcinoma patients through deep learning methodologies. The linear methods LASSO and Elastic Net encounter failure when processing data because they face simultaneous multicollinearity issues in addition to overfitting effects and produce marginal survival outcome variability prediction at 54%. We suggest combining ISIS with deep learning architectures featuring PCA-RFA-RSIS models as a remedy to handle these present limitations. Among all evaluated methods PCA-RFA-RSIS is proved most accurate with an MSE measurement of 24.39 and R2 value of 0.89. PCA improved the model’s dimensionality reduction power and robust ISIS maintained model stability despite outliers present in the data. The discovery holds significant value in precision medicine because it creates opportunities to develop individualized therapy for kidney failure patients. Further research needs to enhance hybrid models and expand their utilization between different diseases as well as complex biological systems.

Dimensions

REFERENCES

[1] A. Spooner, E. Chen, A. Sowmya, P. Sachdev, N.A. Kochan, J. Trollor & H. Brodaty, “A comparison of machine learning methods for survival analysis of high-dimensional clinical data for dementia prediction”, Scientific reports 10 (2020) 20410. https://doi.org/10.1038/s41598-020-77220-w.

[2] S. Salerno & Y. Li, “High-dimensional survival analysis: Methods and applications”, Annual review of statistics and its application 10 (2023) 25. https://doi.org/10.1146/annurev-statistics-032921-022127.

[3] H. Ishwaran, U. B. Kogalur, X. Chen & A. J. Minn, “Random survival forests for high-dimensional data”, Statistical Analysis and Data Mining:’ The ASA Data Science Journal 4 (2011) 115. https://doi.org/10.1002/sam.10103.

[4] S. Wiegrebe, P. Kopper, R. Sonabend,B. Bischl & A. Bender, “Deep learning for survival analysis: a review”, Artificial Intelligence Review 57 (2024) 65. https://doi.org/10.1007/s10462023-10681-3.

[5] P. Wang, Y. Li & C. K. Reddy, “Machine learning for survival analysis: A survey”, ACM Computing Surveys (CSUR) 51 (2019) 1. https://doi.org/10.1145/3214306.

[6] R. Tibshirani, “Regression shrinkage and selection via the lasso”, Journal of the Royal Statistical Society Series B: Statistical Methodology 58 (1996) 267. https://doi.org/10.1111/j.1467-9868.2011.00771.x.

[7] H. Chamlal, A. Benzmane & T. Ouaderhman, “Elastic net-based high dimensional data selection for regression”, Expert Systems with Applications 244 (2024) 122958. https://doi.org/10.1016/j.eswa.2023.122958.

[8] J. Fan & J. Lv, “Sure independence screening for ultrahigh dimensional feature space”, Journal of the Royal Statistical Society Series B: Statistical Methodology 70 (2008) 849. https://doi.org/10.1111/j.1467-9868.2008.00674.x.

[9] R. Reese, X. Dai & G. Fu, “Strong sure screening of ultra-high dimensional categorical data”, arXiv preprint (2018) arXiv:1801.03539. https://arxiv.org/abs/1801.07785.

[10] Z. Ba, Y. Xiao, M. He, D. Liu, H. Wang, H. Liang & J. Yuan, “Risk factors for the comorbidity of hypertension and renal cell carcinoma in the cardio-oncologicera and treatment for tumor-induced hypertension”, Frontiers in Cardiovascular Medicine 9 (2022) 810262. https://doi.org/10.3389/fcvm.2022.810262.

[11] F. Hamad & N. N. Kachouie, “A hybrid method to estimate the full parametric hazard model”, Communications in Statistics-Theory and Methods 48 (2019) 5477. https://doi.org/10.1080/03610926.2018.1513149.

[12] M. Li & B. Ashuri, “Proportional cox hazards model to quantify the likelihood of underestimation in transportation projects”, Journal of Construction Engineering and Management 147 (2021) 04021134. https://doi.org/10.1061/(ASCE)CO.1943-7862.0002164.

[13] Z. Y. Li, Q. Shen, J. Tuo, D. D. Tang, L. G. Zhao, and Y. B. Xiang, “Choice and application of time scale selection for Cox proportional hazards regression model in cohort studies”, Chin Med J (Engl) 43 (2022) 2002. https://doi.org/10.3760/cma.j.cn112338-20220720-00644.

[14] K. Omae & S. Eguchi, “Quasi-linear cox proportional hazards model with cross-l 1 penalty”, BMC Medical Research Methodology 20 (2020) 1.

https://doi.org/10.1186/S12874-020-01063-2.

[15] Z. Lu, S. Wu, D. Ni, M. Zhou, T. Wang, X. Zhou, L. Huang & Y. Yan, “Survival analysis of clear cell renal cell carcinoma based on radiomics and deep learning features from ct images”, Medicine 103 (2024) 40723. https://doi.org/10.1097/md.0000000000040723.

[16] N. Salma, A. H. M. Al-Rammahi & M. K. M. Ali, “A novel feature selection method for ultra high dimensional survival data”, Malaysian Journal of Fundamental and Applied Sciences 20 (2024) 1149. https://doi.org/10.11113/mjfas.v20n5.3665.

[17] F. Y. Chin & Y. K. Goh, “Enhancing classification in high-dimensional data with robust rmi-svm feature selection”, Bulletin of Electrical Engineering and Informatics 13 (2024) 3644. https://doi.org/10.11591/eei.v13i5.7938.

[18] W. Ying, D. Wang, H. Chen & Y. Fu, “Feature selection as deep sequential generative learning”, ACM Transactions on Knowledge Discovery from Data 18 (2024) 1. https://doi.org/10.1145/3687485.

[19] S. Kundu, N. Roy, R. Talukdar, S. Das, S. Mukhopadhyay & B. Basu Mallik, “Ra f 2net: Automated grading of renal cell carcinoma utilizing attention-enhanced deep learning models through feature fusion”, bioRxiv (2024) 2024–07. https://doi.org/10.1101/2024.07.22.604646.

[20] F. Wang, K. Jia & Y. Li, “Integrative deep learning with prior assisted feature selection”, Statistics in Medicine 43 (2024) 3792. https://doi.org/10.1002/sim.10148.

[21] M. V. Ness & M. Udell, “Interpretable Prediction and Feature Selection for Survival Analysis”, (2024). https://doi.org/10.48550/arxiv.2404.14689.

[22] Y. Wang, X. Chen, N. Tang, M. Guo & D. Ai, “Boosting clear cell renal carcinoma-specific drug discovery using a deep learning algorithm and single-cell analysis”, International Journal of Molecular Sciences 25 (2024) 4134. https://doi.org/10.3390/ijms25074134.

[23] P. Le, X. Gong, L. Ung, H. Yang, B. P. Keenan, L. Zhang & T. He, “A robust ensemble feature selection approach to prioritize genes associated with survival outcome in high-dimensional gene expression data”, Frontiers in systems biology 4 (2024) 1355595. https://doi.org/10.3389/fsysb.2024.1355595.

[24] M. Mahootiha, H. A. Qadir, J. Bergsland & I. Balasingham, “Multi-modal deep learning for personalized renal cell carcinoma prognosis: Integrating ct imaging and clinical data”, Computer Methods and Programs in Biomedicine 244 (2024) 107978. https://doi.org/10.48550/arXiv.2307.03575.

[25] H. Ishwaran, U. B. Kogalur, X. Chen & A. J. Minn, “Random survival forests for high-dimensional data”, Statistical Analysis and Data Mining: The ASA Data Science Journal 4 (2011) 115. https://doi.org/10.1002/sam.10103.

[26] M. L. Briceno, “A hybrid methodology for the cox proportional hazard model”, Economia 33 (2008) 179. https://ideas.repec.org/a/ula/econom/v33y2008i26p179-188.html.

[27] B. Guo & N. Yi, “A scalable and flexible Cox proportional hazards model for highdimensional survival prediction and functional selection”, (2022). https://arxiv.org/abs/2205.11600.

[28] J. Jiang & J. Shang, “Feature screening for high-dimensional variable selection in generalized linear models”, Entropy 25 (2023) 851. https://doi.org/10.3390/e25060851.

[29] C. M. O’Brien, “Statistical learning with sparsity: the lasso and generalizations”, (2016). https://deepblue.lib.umich.edu/bitstream/handle/2027.42/119115/insr12167.pdf?sequence=1.

[30] J. Huang, J. L. Horowitz & F. Wei, “Variable selection in nonparametric additive models”, Annals of statistics 38 (2010) 2282. https://doi.org/10.1214/09-AOS781.

[31] Z. Zhang, C.M.M. Padilla, X. Luo, D. Wang & O. H. M. Padilla, “Dense ReLU Neural Networks for Temporal-spatial Model’”, (2025). https://arxiv.org/abs/2411.09961.

[32] A.M. Javid, S. Das, M. Skoglund & S. Chatterjee, “A relu dense layer to improve the performance of neural networks”, In: ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), (2021) 2810. https://doi.org/10.1109/ICASSP39728.2021.9414269.

[33] C. Wang, H. Ma, X. Zhang, X. Xiang, J. Shi, X. Liang, R. Zhao & G. Han, “Deciphering rod pump anomalies: a deep learning autoencoder approach”, Processes 12 (2024) 1845. https://doi.org/10.3390/pr12091845.

[34] H. Abdi & L. J. Williams, “Principal component analysis”, Wiley inter-disciplinary reviews: computational statistics 2 (2010) 433. https://doi.org/10.1002/wics.101.

[35] T. Bankole-Oye, I. El-Thalji & J. Zec, “Combined principal component analysis and proportional hazard model for optimizing condition based maintenance”, IOP Conference Series: Materials Science and Engineering, IOP Publishing 1201 (2021) 012088. https://doi.org/10.1088/1757-899x/1201/1/012088.

[36] H. Peng, N. Pappas, D. Yogatama, R. Schwartz, N. A. Smith & L. Kong, “Random Feature Attention”, (2021). http://arxiv.org/abs/2103.02143.

[37] D.R. Cox, “Regression models and life-tables”, Journal of the Royal Statistical Society: Series B (Methodological) 34 (1972) 187. https://doi.org/10.1111/j.2517-6161.1972.tb00899.x.

[38] A. H. AL-Rammahi & T. R. Dikheel, “Freund’s model with iterated sure independence screening in cox proportional hazard model”, AIP Conference Proceedings, AIP Publishing 2398 (2022) 060009. https://doi.org/10.1063/5.0093464.

[39] Y. Da Wang, M. J. Blunt, R. T. Armstrong & P. Mostaghimi, “Deep learning in pore scale imaging and modeling”, Earth-Science Reviews 215 (2021) 103555. https://doi.org/10.1016/j.earscirev.2021.103555.

[40] H. Abdi, L. J. Williams, “Principal component analysis”, Wiley interdisciplinary reviews: computational statistics 2 (2010) 433. https://doi.org/10.1002/wics.101.

[41] M. N. Yarahmadi, S. A. MirHassani & F. Hooshmand, “Handling the significance of regression coefficients via optimization”, Expert Systems with Applications 238 (2024) 121910. https://doi.org/10.1016/j.eswa.2023.121910.

[42] D. Chicco, M. J. Warrens & G. Jurman, “The coefficient of determination r-squared is more informative than smape, mae, mape, mse and rmse in regression analysis evaluation”, Peerj computer science 7 (2021) 623. https://doi.org/10.7717/peerj-cs.623.

[43] L. Zhang, J. Zhang, W. Gao, F. Bai, N. Li & N. Ghadimi, “A deep learning outline aimed at prompt skin cancer detection utilizing gated recurrent unit networks and improved orca predation algorithm”, Biomedical Signal Processing and Control 90 (2024) 105858. https://doi.org/10.1016/j.bspc.2023.105858.

[44] C. D. Lewis, “Industrial and business forecasting methods: A practical guide to exponential smoothing and curve fitting”, (1982). https://cir.nii.ac.jp/crid/1130282269656766080.