Implementing a dung beetle optimization algorithm enhanced with multi-strategy fusion techniques

xiaojie zhou; Majid Khan Majahar Ali; Farah Aini Abdullah; Lili Wu; Ying Tian; Tao Li; Kaihui Li

doi:10.46481/jnsps.2025.2472

Authors

xiaojie zhou School of Mathematical Sciences, Universiti Sains Malaysia, Pulau Pinang 11800, Malaysia
Majid Khan Majahar Ali
[email protected]
School of Mathematical Sciences, Universiti Sains Malaysia, Pulau Pinang 11800, Malaysia
Farah Aini Abdullah School of Mathematical Sciences, Universiti Sains Malaysia, Pulau Pinang 11800, Malaysia
Lili Wu School of Mathematical Sciences, Universiti Sains Malaysia, Pulau Pinang 11800, Malaysia
Ying Tian School of Mathematical Sciences, Universiti Sains Malaysia, Pulau Pinang 11800, Malaysia
Tao Li School of Mathematical Sciences, Universiti Sains Malaysia, Pulau Pinang 11800, Malaysia
Kaihui Li School of Mathematical Sciences, Universiti Sains Malaysia, Pulau Pinang 11800, Malaysia

Keywords:

Dung beetle optimization algorithm, Golden sine algorithm, Self-Spiral Strategy, Levy flight, Adaptive t-distribution

Abstract

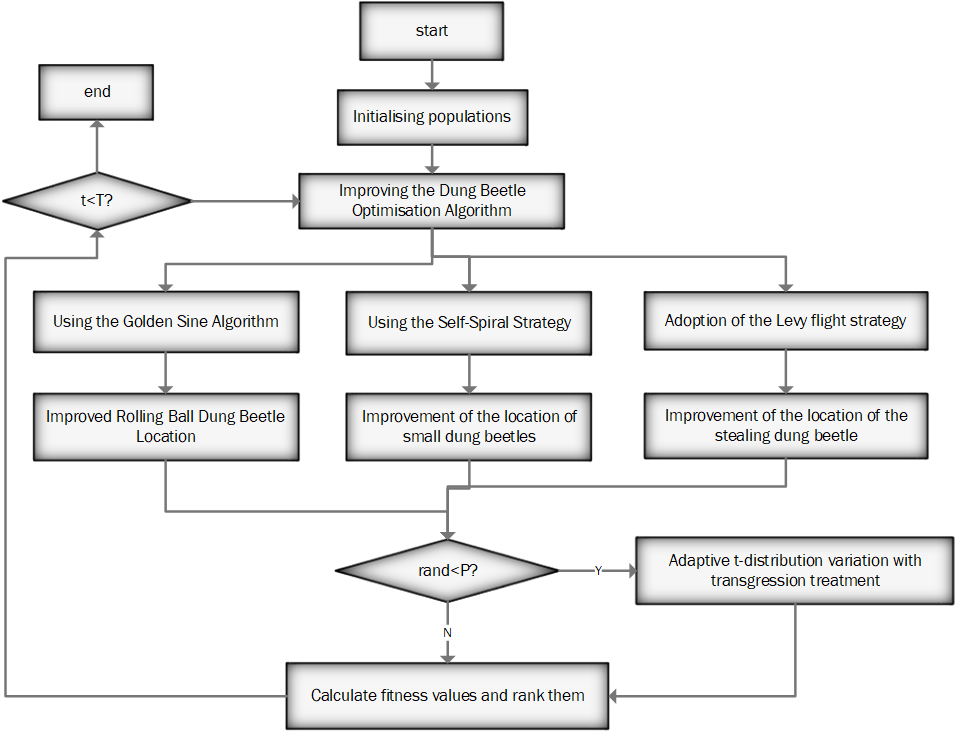
The dung beetle optimization algorithm possesses robust search and optimization capabilities. However, when it encounters complex optimization challenges, it struggles with limited accuracy, restricted global search ability, and suboptimal results from iterative optimization processes. To address these limitations, this study introduces a multi-strategy improved dung beetle optimization algorithm (CDBO). Initially, the golden sine method is implemented during the rolling phase to improve the algorithm’s capacity for both late area mining and early broad exploration; Then, in order to move the population closer to the ideal location during the foraging phase, the self-spiral method of the whale optimization algorithm is adopted. In the meanwhile, the present optimal location is arbitrarily perturbed during the stealing phase by introducing the flight of Levy strategy; Ultimately, the global optimal solution is modified using the dynamic t-distribution to enhance the algorithm’s capacity to eliminate the regional optimal solution. This study presents simulation tests with other intelligent optimisation algorithms on 23 test functions. The outcomes demonstrate that when the dimension is 30, the enhanced method performs optimally on at least 21 test functions. The modified method still earns the top score on 22 test functions and keeps its great search capabilities when the dimension is raised to 100. The enhanced approach is applied to address K-means clustering and engineering optimization problems to further assess its potential. The findings indicate that the improved method significantly boosts both the convergence rate and the accuracy of the optimization process.

Dimensions

REFERENCES

[1] R. Salgotra, P. Sharma, S. Raju & A. H. Gandomi, “A Contemporary Systematic Review on Meta-heuristic Optimization Algorithms with Their MATLAB and Python Code Reference”, Archives of Computational Methods in Engineering 31 (2024) 1749. https://doi.org/10.1007/s11831-023-10030-1.

[2] J. He & L. Fu, “Robot path planning based on improved dung beetle optimizer algorithm”, J. Braz. Soc. Mech. Sci. Eng. 46 (2024) 235. https://doi.org/10.1007/s40430-024-04768-3.

[3] J. Liu, L. Cong, Y. Xia, G. Pan, H. Zhao & Z. Han, “Short-term power load prediction based on DBO-VMD and an IWOA-BILSTM neural network combination model”, Dianli Xitong Baohu Yu Kongzhi Power Syst. Prot. Control 52 (2024) 123. https://doi.org/10.19783/j.cnki.pspc.231402.

[4] X. Yi & Y. Liu, Multi-model ensemble air quality prediction with dung beetle optimization, presented at the 2023 5th International Conference on Machine Learning, Big Data and Business Intelligence (MLBDBI), 2023, pp. 338–342. https://doi.org/10.1109/MLBDBI60823.2023.10482164.

[5] D. Xu, Z. Li & W. Wang, “An ensemble model for monthly runoff prediction using least squares support vector machine based on variational modal decomposition with dung beetle optimization algorithm and error correction strategy”, J. Hydrol. 629 (2024) 130558. https://doi.org/10.1016/j.jhydrol.2023.130558.

[6] Q. Yuan, L. Wu, Y. Huang, Z. Guo & N. Li, “Water-body detection from spaceborne SAR images with DBO-CNN”, IEEE Geosci. Remote Sens. Lett. 20 (2023) 4013405. https://doi.org/10.1109/LGRS.2023.3325939.

[7] S. Gao, Z. Li, Y. Zhang, S. Zhang & J. Zhou, “Remaining useful life prediction method of rolling bearings based on improved 3 and DBOHKELM”, Meas. Sci. Technol. 35 (2024) 106101. https://iopscience.iop.org/article/10.1088/1361-6501/ad52b5/meta.

[8] D. Zhang, C. Zhang, X. Han & C. Wang, “Improved DBO-VMD and optimized DBN-ELM based fault diagnosis for control valve”, Meas. Sci. Technol. 35 (2024) 075103. https://doi.org/10.1088/1361-6501/ad3be0.

[9] W. Cao, Z. Liu, H. Song, G. Li & B. Quan, “Dung beetle optimized fuzzy PID algorithm applied in four-bar target temperature control system”, Appl. Sci.-Basel 14 (2024) 4168. https://doi.org/10.3390/app14104168

[10] J. Sharma & R. S. Singhal, Comparative research on genetic algorithm, particle swarm optimization and hybrid GA-PSO, Proc. 2nd Int. Conf. Comput. Sustain. Global Dev. (INDIACOM), 2015, pp. 110–114. https://www.webofscience.com/wos/woscc/full-record/WOS:000381554300024.

[11] W. Tong, “A hybrid algorithm framework with learning and complementary fusion features for whale optimization algorithm”, Sci. Program. 2020 (2020) 5684939. https://doi.org/10.1155/2020/5684939.

[12] S. Gupta & K. Deep, ”Enhanced leadership-inspired grey wolf optimizer for global optimization problems”, Eng. Comput. 36 (2020) 1777. https://doi.org/10.1007/s00366-019-00795-0.

[13] J. Xue & B. Shen, ”Dung beetle optimizer: a new meta-heuristic algorithm for global optimization”, J. Supercomput. 79 (2023) 7305. https://doi.org/10.1007/s11227-022-04959-6.

[14] M. Dehghani, S. Hubalovsky & P. Trojovsky, ”Northern goshawk optimization: a new swarm-based algorithm for solving optimization problems”, IEEE Access 9 (2021) 162059. https://doi.org/10.1109/ACCESS.2021.3133286.

[15] X. Kuang, B. Yang, H. Ma, W. Tang, H. Xiao & L. Chen, “Multi-strategy improved dung beetle optimization algorithm”, Comput. Eng., Mar. 2024, Advance online publication, Accessed: Jun. 12, 2024. [Online]. https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CAPJ&dbname=CAPJLAST&filename=JSJC2024022900B.

[16] L. Wang & L. Gu, “Improved dung beetle optimization algorithm with multi-strategy”, Comput. Syst. Appl. 33 (2024) 224. https://doi.org/10.15888/j.cnki.csa.009397.

[17] J. Pan, S. Li, P. Zhou, G. Yang & D. Lv, “Dung beetle optimization algorithm guided by improved sine algorithm”, Comput. Eng. Appl. 59 (2023) 92.

[18] R. Yu, Z. Xu, X. Chen & L. Jiang, “Research on multi-strategy improvement of dung beetle optimization algorithm”, J. Nanning Normal Univ., Apr. 2024, Advance online publication, Accessed: Jun. 30, 2024. [Online]. Available: https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CAPJ&dbname=CAPJLAST&filename=GXSZ20240416004.

[19] F. Zhu, G. Li, H. Tang, Y. Li, X. Lv & X. Wang, “Dung beetle optimization algorithm based on quantum computing and multi-strategy fusion for solving engineering problems”, Expert Syst. Appl. 236 (2024) 121219. https://doi.org/10.1016/j.eswa.2023.121219.

[20] X. Wang, Y. Wei, Z. Guo, J. Wang, H. Yu & B. Hu, “A Sinh-Cosh enhanced DBO algorithm applied to global optimization problems”, Biomimetics 9 (2024) 271. https://doi.org/10.3390/biomimetics9050271.

[21] M. Ye, H. Zhou, H. Yang, B. Hu & X. Wang, “Multi-strategy improved dung beetle optimization algorithm and its applications”, Biomimetics 9 (2024) 291. https://doi.org/10.3390/biomimetics9050291.

[22] X. Wang, H. Kang, Y. Shen, X. Sun & Q. Chen, “An improved dung beetle optimization algorithm for high-dimension optimization and its engineering applications”, Symmetry-Basel 16 (2024) 586. https://doi.org/10.3390/sym16050586.

[23] J. Zhang & J. S. Wang, ”Improved whale optimization algorithm based on nonlinear adaptive weight and golden sine operator”, IEEE Access 8 (2020) 77013. https://doi.org/10.1109/ACCESS.2020.2989445.

[24] R. Rajabioun, “Cuckoo optimization algorithm”, Appl. Soft Comput. 11 (2011) 5508. https://doi.org/10.1016/j.asoc.2011.05.008.

[25] D. T. Cassidy, “Describing n-day returns with Student’s t-distributions”, Phys. Stat. Mech. Appl. 390 (2011) 2794. https://doi.org/10.1016/j.physa.2011.03.019.

[26] Q. Li, H. Shi, W. Zhao & C. Ma, “Enhanced dung beetle optimization algorithm for practical engineering optimization”, Mathematics 12 (2024) 7. https://doi.org/10.3390/math12071084.

[27] H. Ismkhan, “I-k-means-plus: An iterative clustering algorithm based on an enhanced version of the k-means”, Pattern Recognit. 79 (2018) 402. https://doi.org/10.1016/j.patcog.2018.02.015.