Computational optimization of auctioneer revenue in modified discrete Dutch auctions with cara risk preferences

Raja Aqib Shamim; Majid Khan Majahar Ali; Mohamed Farouk Haashir bin Hamdullah

doi:10.46481/jnsps.2026.2516

Authors

Raja Aqib Shamim
School of Mathematical Sciences, Universiti Sains Malaysia, 11800, Pulau Penang, Malaysia

Department of Mathematics, University of Kotli, 11100, Azad Jammu and Kashmir, Pakistan
Majid Khan Majahar Ali
[email protected]

School of Mathematical Sciences, Universiti Sains Malaysia, 11800, Pulau Penang, Malaysia
https://orcid.org/0000-0002-5558-5929
Mohamed Farouk Haashir bin Hamdullah
Kolej Yayasan UEM, Malaysia

Keywords:

Auctions, Lognormal distribution, Nonlinear programming, Discrete Dutch auction, Revenue

Abstract

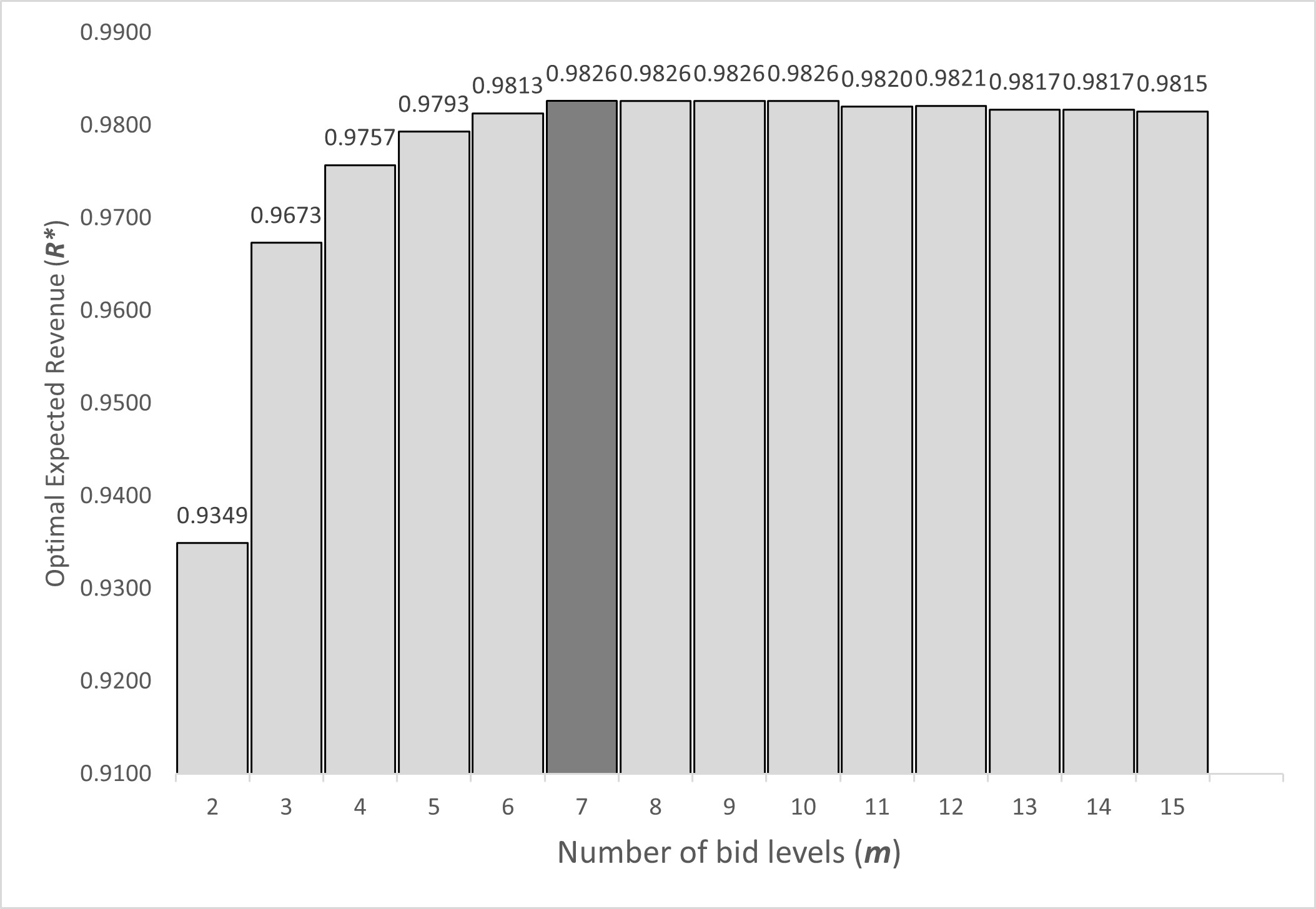
This research presents a computational optimization framework designed to maximize auctioneer revenue in modified discrete Dutch auctions by explicitly incorporating bidders’ risk preferences---modeled independently of wealth through the Constant Absolute Risk Aversion (CARA) utility function---thus enabling the analysis of risk-averse, risk-neutral, and risk-loving behaviors within the auction context. The study models bidders with three distinct risk profiles--risk-loving, risk-neutral, and risk-averse--employing nonlinear programming techniques to optimize expected revenues for the discrete bid levels. Discrete optimization methods are applied to analyze the impact of varying risk preferences, revealing that auctioneer revenue grows nonlinearly with bidder participation. For risk-neutral bidders (\alpha -> 0), revenue increases sharply from \mathscr{R}^* = 0.3849 for n=2 to \mathscr{R}^* = 0.8179 for n = 20 (a 112.5% increase), but the rate of growth declines significantly beyond n=30, with revenue plateauing near \mathscr{R}^* = 0.9454 for n = 100 (a mere 9.5\% increase from n = 30 to n = 100). Similar patterns hold for risk-averse (\alpha > 0) and risk-loving (\alpha < 0) bidders, though the magnitudes differ. Moreover, risk-loving bidders (for \alpha = -0.5) yield \mathscr{R}^* = 1.2122 for n = 100, a 28\% higher revenue than risk-neutral case with \mathscr{R}^*= 0.9454 and a 61% higher than risk-averse case (for \alpha = 0.5) with \mathscr{R}^*=0.7519. This nonlinearity suggests diminishing marginal returns to additional bidders, a critical insight for auction design. The findings suggest that for larger bidder groups, fewer bid levels are sufficient for revenue maximization, with risk-averse behavior decreasing expected returns and risk-loving behavior amplifying them. This computational approach highlights the critical role of risk preferences in auction design, offering a robust mathematical model that can be adapted for broader applications in algorithmic auction mechanisms.

Dimensions

REFERENCES

[1] D. Shannon, M. Dowling, M. Zhaf & B. Sheehan, “Dutch auction dynamics in non-fungible token (NFT) markets”, Economic Modelling 141 (2024) 106882. https://doi.org/10.1016/j.econmod.2024.106882.

[2] J. Bobulski & S. Szymoniak, “Deep Learning Method for Classifying Items into Categories for Dutch Auctions”, Computer Assisted Methods in Engineering and Science 31 (2024) 67. http://dx.doi.org/10.24423/cames.2024.979.

[3] W. Vickrey, “Counterspeculation, auctions, and competitive sealed tenders”, The Journal of Finance 16 (1961) 8. http://dx.doi.org/10.1111/j.1540-6261.1961.tb02789.x.

[4] E. Karni, “On the equivalence between descending bid auctions and first price sealed bid auctions”, Theory and Decision 25 (1988) 211. https://doi.org/10.1007/BF00133162.

[5] D. Lucking-Reiley, “Using field experiments to test equivalence between auction formats: Magic on the internet”, American Economic Review 89 (1999) 1063. https://doi.org/10.1257/aer.89.5.1063.

[6] P. Miettinen, “Information acquisition during a dutch auction”, Journal of Economic Theory 148 (2013) 1213. https://doi.org/10.1016/j.jet.2012.09.018.

[7] B. Balzer & A. Rosato, “Expectations-based loss aversion in auctions with interdependent values: Extensive vs. intensive risk”, Management Science 67 (2021) 1056. https://doi.org/10.1287/mnsc.2019.3563.

[8] J. G. Riley & W. F. Samuelson, “Optimal auctions”, The American Economic Review 71 (1981) 381. https://www.jstor.org/stable/1802786.

[9] E. Maskin & J. Riley, “Asymmetric auctions”, The Review of Economic Studies 67 (2000) 413. https://doi.org/10.1111/1467-937X.00137.

[10] E. Katok & A. M. Kwasnica, “Time is money: The effect of clock speed on seller’s revenue in dutch auctions”, Experimental Economics 11 (2008) 344. https://doi.org/10.1007/s10683-007-9169-x.

[11] Z. Li & C.-C. Kuo, “Revenue-maximizing dutch auctions with discrete bid levels”, European Journal of Operational Research 215 (2011) 721. https://doi.org/10.1016/j.ejor.2011.05.039.

[12] Z. Li & C.-C. Kuo, “Design of discrete dutch auctions with an uncertain number of bidders”, Annals of Operations Research 211 (2013) 255. https://doi.org/10.1007/s10479-013-1331-6.

[13] Z. Li, J. Yue & C.-C. Kuo, “Design of discrete dutch auctions with consideration of time”, European Journal of Operational Research 265 (2018) 1159. https://doi.org/10.1016/j.ejor.2017.08.043.

[14] O. Carare & M. Rothkopf, “Slow dutch auctions”, Management Science 51 (2005) 365. https://doi.org/10.1287/mnsc.1040.0328.

[15] T. E. Rockoff & M. Groves, “Design of an internet-based system for remote dutch auctions”, Internet Research 5 (1995) 10. https://doi.org/10.1108/EUM0000000006756.

[16] K. Naboureh, A. Makui, S. J. Sajadi & E. Safari, “Online hybrid dutch auction with both private and common value components and counteracting overpayments”, Electronic Commerce Research and Applications 59 (2023) 101247. https://doi.org/10.1016/j.elerap.2023.101247.

[17] J. C. Cox, V. L. Smith & J. M. Walker, “Auction market theory of heterogeneous bidders”, Economics Letters 9 (1982) 319. http://dx.doi.org/10.1016/0165-1765(82)90038-6.

[18] A. Hu, S. A. Matthews & L. Zou, “Risk aversion and optimal reserve prices in first- and second-price auctions”, Journal of Economic Theory 145 (2010) 1188. http://dx.doi.org/10.1016/j.jet.2010.02.006.

[19] A. Makui, K. Naboureh & S. J. Sadjadi, “An experimental study of auctions behavior with risk preferences”, International Journal of Industrial Engineering and Management Science 8 (2021) 1. https://doi.org/10.22034/ijiems.2022.360921.1057.

[20] R. A. Shamim & M. K. M. Ali, “Optimizing discrete dutch auctions with time considerations: a strategic approach for lognormal valuation distributions”, Journal of the Nigerian Society of Physical Sciences 7 (2021) 2291. https://doi.org/10.46481/jnsps.2025.2291.

[21] A. Henriques, N. Aleixo, P. Elson, J. Devine, G. Azzopardi, M. Andreini, M. Rognlien, N. Tarocco, J. Tang, “Modelling airborne transmission of SARS-CoV-2 using CARA: risk assessment for enclosed spaces”, Interface Focus 12 (2022) 20210076. https://doi.org/10.1098/rsfs.2021.0076.

[22] B. Jullien, B. Salanie & F. Salanie, “Screening risk-averse agents under moral hazard: single-crossing and the CARA case”, Economic Theory 30 (2007) 151. https://doi.org/10.1007/s00199005-0040-z.

[23] S. Matthews, “Comparing auctions for risk averse buyers: A buyer’s point of view”, Econometrica 55 (1987) 633. http://dx.doi.org/10.2307/1913603.

[24] C. Brunner, A. Hu & J. Oechssler, “Premium auctions and risk preferences: an experimental study”, Games and Economic Behavior 87 (2014) 467. https://doi.org/10.1016/j.geb.2014.06.002.

[25] J. Delnoij & K. De Jaegher, “Competing first-price and second-price auctions”, Economic Theory 69 (2020) 183. https://doi.org/10.1007/s00199-018-1161-5.

[26] J.-P. Chavas, Risk analysis in theory and practice, Elsevier Academic Press, California, USA, 2004, pp. 139–160. https://shop.elsevier.com/books/risk-analysis-in-theory-and-practice/chavas/978-0-12-170621-0.

[27] D. J. Meyer & J. Meyer, “Relative risk aversion: What do we know?”, Journal of Risk and Uncertainty 31 (2005) 243. https://doi.org/10.1007/s11166-005-5102-x.

[28] P. R. Milgrom, Putting auction theory to work, Cambridge University Press, Cambridge, United Kingdom, 2003, pp. 157–204. https://catdir.loc.gov/catdir/samples/cam041/2003051544.pdf.

[29] V. Krishna, Auction theory, Academic press, Burlington, USA, 2009, pp. 38–41. https://bugarinmauricio.com/wp-content/uploads/2017/06/krishna-auction-theory-caps1a4.pdf.

[30] F. Alvarez & C. Mazon, “Comparing the spanish and the discriminatory auction formats: A discrete model with private information”, European Journal of Operational Research 179 (2007) 253. https://doi.org/10.1016/j.ejor.2006.02.044.

[31] P. Murto & J. Valimaki, “Large common value auctions with risk averse bidders”, Games and Economic Behavior 91 (2015) 60. https://doi.org/10.1016/j.geb.2015.03.015.

[32] T. Mathews, “Bidder welfare in an auction with a buyout option”, International Game Theory Review 8 (2006) 595. https://doi.org/10.1142/S0219198906001132.

[33] A. S. Pekec & I. Tsetlin, “Revenue ranking of discriminatory and uniform auctions with an unknown number of bidders”, Management Science 54 (2008) 1610. https://doi.org/10.1287/mnsc.1080.0882.

[34] W. H. Yuen, C. W. Sung & W. S. Wong, “Optimal price decremental strategy for dutch auctions”, Communications in Information and Systems 2 (2002) 411. http://dx.doi.org/10.4310/CIS.2002.v2.n4.a6.

[35] M. Rabin, Risk aversion and expected-utility theory: A calibration theorem, in Handbook of the fundamentals of financial decision making: Part I, Leonard C MacLean (Ed.) & William T Ziemba (Ed.), World Scientific Publishing, Singapore, 2013, pp. 241–252. https://doi.org/10.1142/9789814417358 0013.

[36] B. A. Babcock, E. K. Choi & E. Feinerman, “Risk and probability premiums for CARA utility functions”, Journal of Agricultural and Resource Economics 18 (1993) 17. http://dx.doi.org/10.22004/ag.econ.30810.

[37] L. Yong & L. Shulin, “Effects of risk aversion on all-pay auction with reimbursement”, Economics Letters 185 (2019) 108751. https://doi.org/10.1016/j.econlet.2019.108751.

[38] S. Vasserman & M. Watt, “Risk aversion and auction design: Theoretical and empirical evidence”, International Journal of Industrial Organization 79 (2021) 102758. https://doi.org/10.1016/j.ijindorg.2021.102758.

[39] O. Bos, F. Gomez-Martinez & S. Onderstal, “Signalling in auctions for risk-averse bidders”, PLoS One 17 (2022) e0275709. https://doi.org/10.1371/journal.pone.0275709.