Collocation Approach for the Computational Solution Of Fredholm-Volterra Fractional Order of Integro-Differential Equations
Keywords:
FREDHOLM-VOLTERRA, Collocation, Integro-differentialAbstract
In this work, a collocation technique is used to determine the computational solution to fractional order Fredholm-Volterra integro-differential equations with boundary conditions using Caputo sense. We obtained the linear integral form of the problem and transformed it into a system of linear algebraic equations using standard collocation points. The matrix inversion approach is adopted to solve the algebraic equation and substituted it into the approximate solution. We established the uniqueness and convergence of the method and some modelled numerical examples are provided to demonstrate the method’s correctness and efficiency. It is observed that the results obtained by our new method are accurate and performed better than the results obtained in the literature. The study will be useful to engineers and scientists. It is advantageous because it addresses the difficulty in tackling fractional order Fredholm-Volterra integro-differential problems using a simple collocation strategy. The approach has the advantage of being more accurate and reducing computer running time.
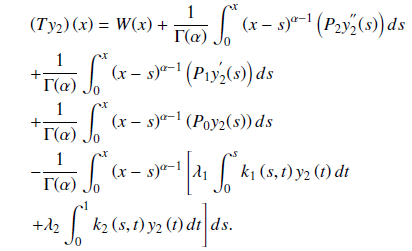
Published
How to Cite
Issue
Section
Copyright (c) 2022 Ganiyu Ajileye, Adewale James, Ayinde Abdullahi, Taiye Oyedepo

This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
Similar Articles
- I. R. Silviya, K. Muthunagai, Differential and fuzzy differential sandwich theorems involving quantum calculus operators , Journal of the Nigerian Society of Physical Sciences: Volume 6, Issue 1, February 2024
- Kashif Hussain, Oluwaseun Adeyeye, Nazihah Ahmad, Numerical Solution of Second Order Fuzzy Ordinary Differential Equations using Two-Step Block Method with Third and Fourth Derivatives , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 2, May 2023
- Felix Yakubu Eguda, Andrawus James, Sunday Babuba, The Solution of a Mathematical Model for Dengue Fever Transmission Using Differential Transformation Method , Journal of the Nigerian Society of Physical Sciences: Volume 1, Issue 3, August 2019
- Jamilu Adamu, Aminu Sulaiman Halliru, Bala Ma’aji Abdulhamid, On Some Pursuit Differential Game Problem in a Hilbert Space , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 1, February 2022
- Gurpreet Tuteja, Tapshi Singh, Comments on “The Solution of a Mathematical Model for Dengue Fever Transmission Using Differential Transformation Method: J. Nig. Soc. Phys. Sci. 1 (2019) 82-87” , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 2, May 2021
- Kazeem adebowale Dawodu, Extension of ADMMAlgorithmin Solving Optimal Control Model Governed by Partial Differential Equation , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 2, May 2021
- Abbas Ja'afaru Badakaya, Bilyaminu Muhammad, A Purusit Differential Game Problem on a Closed Convex Subset of a Hilbert Space , Journal of the Nigerian Society of Physical Sciences: Volume 2, Issue 3, August 2020
- O. M. Ogunlaran, M. A. Kehinde, M. A. Akanbi, E. I. AKINOLA, A Chebyshev polynomial based block integrator for the direct numerical solution of fourth order ordinary differential equations , Journal of the Nigerian Society of Physical Sciences: Volume 6, Issue 2, May 2024
- Rachid El chaal, Hamid Dalhi, Otmane Darbal, Omar Boughaleb, Analytical resolution of nonlinear fractional equations using the GERDFM method: Application to nonlinear Schrödinger and truncated Boussinesq-Burgers equations , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 4, November 2025
- Lamees K. Alzaki, Hassan Kamil Jassim, Time-Fractional Differential Equations with an Approximate Solution , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 3, August 2022
You may also start an advanced similarity search for this article.
Most read articles by the same author(s)
- G. Ajileye, A. A. James, Collocation Method for the Numerical Solution of Multi-Order Fractional Differential Equations , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 3, August 2023






