Mathematical Modeling of Waves in a Porous Micropolar Fibrereinforced Structure and Liquid Interface
Keywords:
Micropolar, Fibre reinforced, Reflection/transmission, Voids/porosity, Liquid interfaceAbstract
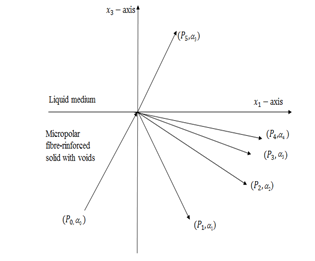
The present investigation envisages on the Mathematical modeling of waves propagating in a porous micropolar fibre-reinforced structure in a half-space and liquid interface. The harmonic method of wave analysis is utilized, such that, the reflection and transmission of waves in the media were modelled and it’s equations of motion analytically derived. It was deduced that incident longitudinal wave in the solid structure yielded four reflected waves given as; quasi–P wave (qLD), quasi–SV wave, quasi–transverse microrotational (qTM) wave and a wave due to voids and one transmitted wave known as the quasi-longitudinal transmitted (qLT) wave. The phase velocity in the liquid medium is independent of angle of propagation as observed. The corresponding amplitude ratios of propagations for both reflected and transmitted waves are analytically derived by employing Snell’s law. The model would prove to be of relevance in the understanding of modeling of the behavior of propagation phenomena of waves in micropolar fibre-reinforecd machination systems resulting in solid/liquid interfaces especially in earth sciences and in particular seismology, amongst others.
Published
How to Cite
Issue
Section
Copyright (c) 2022 Augustine Igwebuike Anya, Uko Ofe, Aftab Khan

This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
Similar Articles
- S. Alao , R. A. Oderinu, B. A. Sanusi, T. A. Oyeyinka, F. J. Ayanbukola, Computational investigation of magnetohydrodynamics Casson Micropolar fluid flowing past a permeable linearly stretchy wall with heat source , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 3, August 2025
- S. S. Aladodo, C. O. Akoshile, J. O. Otu, A Review of Evidence of Aerosol Transmission of SARS-CoV-2 Particles , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 3, August 2021
- Pragati, Rajneesh Kumar, Sachin Kaushal, Effect of a moving thermal load in a modified couple stress medium with double porosity and hyperbolic two-temperature theory , Journal of the Nigerian Society of Physical Sciences: Volume 8, Issue 1, February 2026 (In Progress)
- Akindeji Opeyemi Fajana, Adam Muhammed Olawale, Hammed Ajibola Oyesomi, Quantitative reservoir evaluation and hydrocarbon volumetrics :an integrated petrophysical and 3-D static modeling approach in ‘Hamphidex’ field, Niger-Delta, Nigeria , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 2, May 2025
- James Andrawus, Kayode Isaac Omotoso, Agada Apeh Andrew, Felix Yakubu Eguda, Sunday Babuba, Kabiru Garba Ibrahim, Mathematical model analysis on the significance of surveillance and awareness on the transmission dynamics of diphtheria , Journal of the Nigerian Society of Physical Sciences: Volume 7, Issue 4, November 2025
- Gurpreet Tuteja, Tapshi Singh, Comments on “The Solution of a Mathematical Model for Dengue Fever Transmission Using Differential Transformation Method: J. Nig. Soc. Phys. Sci. 1 (2019) 82-87” , Journal of the Nigerian Society of Physical Sciences: Volume 3, Issue 2, May 2021
- K. Manickavelan, S. Ahmed, K. Mithun, P. Sathish, R. Rajasekaran , N. Sellappan, A review on Transforming plastic wastes into fuel , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 1, February 2022
- S. O. Salawu, R. A. Kareem, J. O. Ajilore, Eyring-Powell MHD nanoliquid and entropy generation in a porous device with thermal radiation and convective cooling , Journal of the Nigerian Society of Physical Sciences: Volume 4, Issue 4, November 2022
- Abdulaziz G. Ahmad, Nnamdi F. Okechi, David U. Uche, Abdulwasiu O. Salaudeen, Numerical Simulation of Nonlinear and Non-Isothermal Liquid Chromatography for Studying Thermal Variations in Columns Packed with Core-Shell Particles , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 2, May 2023
- Essodossomondom Anate, N’Detigma Kata, Hodo-Abalo Samah, Amadou Seidou Maiga, Study of the passivation of defects in the perovskite cell: application to Sahelian climate conditions , Journal of the Nigerian Society of Physical Sciences: Volume 5, Issue 2, May 2023
You may also start an advanced similarity search for this article.






